题目内容
17.在正项等比数列{an}中,若3a1,$\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_{2014}}-{a_{2015}}}}{{{a_{2016}}-{a_{2017}}}}$=$\frac{1}{9}$.分析 设正项等比数列{an}的公比为q>0,根据3a1,$\frac{1}{2}{a_3},2{a_2}$成等差数列,可得:2×$\frac{1}{2}{a}_{3}$=3a1+2a2,即${a}_{1}{q}^{2}$=3a1+2a1q,解出q,再利用等比数列的通项公式即可得出.
解答 解:设正项等比数列{an}的公比为q>0,∵3a1,$\frac{1}{2}{a_3},2{a_2}$成等差数列,
∴2×$\frac{1}{2}{a}_{3}$=3a1+2a2,即${a}_{1}{q}^{2}$=3a1+2a1q,
∴q2-2q-3=0,q>0,
解得q=3.
则$\frac{{{a_{2014}}-{a_{2015}}}}{{{a_{2016}}-{a_{2017}}}}$=$\frac{{a}_{2014}-{a}_{2015}}{{q}^{2}({a}_{2014}-{a}_{2015})}$=$\frac{1}{9}$.
故答案为:$\frac{1}{9}$.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知x>0,y>0,x+y+$\sqrt{xy}$=2,则x+y的最小值是( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
12.等比数列{an}中,a2=9,a5=243,则a1与a7的等比中项为( )
| A. | ±81 | B. | 81 | C. | -81 | D. | 27 |
7.已知全集为R,集合A={x|$\frac{x-1}{x}$<0},B={x|x≥1},则A∪B等于( )
| A. | {x|x>0} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|x≤0} |
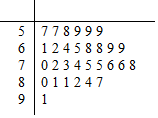 2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会(简称冬奥会)在北京和张家口两个城市举办.某中学为了普及奥运会知识,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.
2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会(简称冬奥会)在北京和张家口两个城市举办.某中学为了普及奥运会知识,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.