题目内容
等比数列{an}的公比q>1,且a1+a2+a3=7,a1a2a3=8,求:
(1)a1+a3的值;
(2)数列{an}前8项的和S8.
(1)a1+a3的值;
(2)数列{an}前8项的和S8.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知列式求出等比数列的首项和公比,进一步求出a3,则a1+a3的值可求;
(2)直接由等比数列的前n项和求得数列{an}前8项的和S8.
(2)直接由等比数列的前n项和求得数列{an}前8项的和S8.
解答:
解:(1)由a1a2a3=8,得a23=8,即a2=2,
代入a1+a2+a3=7,得a1+2+a1q2=7,a1+a1q2=5,
又a2=a1q=2,解得:q=
(舍)或q=2.
∴a1=1,则a3=a1q2=1×22=4,
∴a1+a3=1+4=5;
(2)S8=
=255.
代入a1+a2+a3=7,得a1+2+a1q2=7,a1+a1q2=5,
又a2=a1q=2,解得:q=
| 1 |
| 2 |
∴a1=1,则a3=a1q2=1×22=4,
∴a1+a3=1+4=5;
(2)S8=
| 1×(1-28) |
| 1-2 |
点评:本题考查了等比数列的通项公式,考查了等比数列的前n项和,是基础的计算题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
设集合A={x|x2-2x=0},B={x|y=
,x∈N},则A∩B=( )
| x+1 |
| A、{0,1,2} |
| B、{0,-1,2} |
| C、{0,2} |
| D、{0} |
命题“若x∈N*,则x2≥0”的逆命题,否命题,逆否命题中,正确的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
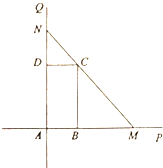 如图,互相垂直的两条公路AP,AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=10m,AD=20m,记三角形花园AMN的面积为S,
如图,互相垂直的两条公路AP,AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=10m,AD=20m,记三角形花园AMN的面积为S,