题目内容
17.同时掷两粒骰子(六个面分别标有1,2,3,4,5,6个点的正方体),则向上的点数之和为3的倍数的概率为$\frac{1}{3}$.分析 同时掷两粒骰子(六个面分别标有1,2,3,4,5,6个点的正方体),先求出基本事件总数,再由列举法求出向上的点数之和为3包含的基本事件个数,由此能求出向上的点数之和为3的倍数的概率.
解答 解:同时掷两粒骰子(六个面分别标有1,2,3,4,5,6个点的正方体),
基本事件总数n=6×6=36,
向上的点数之和为3包含的基本事件有:
(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),(3,3),(3,6),(6,3),(4,5),(5,4),(6,6),
其12个,
∴向上的点数之和为3的倍数的概率为p=$\frac{12}{36}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.抛物线x2-4y=0的准线方程是( )
| A. | y=-1 | B. | y=-$\frac{1}{16}$ | C. | x=-1 | D. | x=-$\frac{1}{16}$ |
2.已知$sinα=\frac{3}{5}$,则sin(α+π)=( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
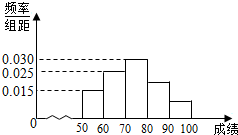 某校共有400名学生参加了一次数学竞赛,竞赛成绩都在[50,100]内,且频率分布直方图如图所示(成绩分组为[50,60],[60,70],[70,80),[80,90),[90,100]),则在本次竞赛中,得分不低于80分的人数为120.
某校共有400名学生参加了一次数学竞赛,竞赛成绩都在[50,100]内,且频率分布直方图如图所示(成绩分组为[50,60],[60,70],[70,80),[80,90),[90,100]),则在本次竞赛中,得分不低于80分的人数为120.