题目内容
已知函数f（x）=sinx，则f′（
）= ．
| π |
| 2 |
考点：导数的运算
专题：导数的概念及应用
分析：根据导数的基本公式计算即可．
解答：
解：∵f（x）=sinx，
∴f′（x）=cosx，
∴f′（
）=cos
=0，
故答案为：0
∴f′（x）=cosx，
∴f′（
| π |
| 2 |
| π |
| 2 |
故答案为：0
点评：本题主要考查了常用的函数的导数，属于基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
三个平面最多可以把空间分成（ ）
| A、4部分 | B、6部分 |
| C、7部分 | D、8部分 |
设F1，F2分别是双曲线
-
=1（a＞0，b＞0）的左、右焦点，若双曲线左支上存在一点M使
•（
+
）=0，O坐标原点，且|
|=
|
|，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| OM |
| OF1 |
| MF1 |
| ||
| 3 |
| MF2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知F1（-3，0），F2（3，0），是椭圆
+
=1（a＞b＞0）两个焦点，P在椭圆上，∠F1PF2=α，且当α=
时，△F1PF2的面积最大，则椭圆的标准方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
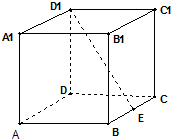如图在棱长为2的正方体ABCD-A1B1C1D1中E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|