题目内容
 如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,
如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,(Ⅰ)求证:平面ABE⊥平面BCF;
(Ⅱ)若平面BEF与平面BCF所成的二面角为60°,求圆柱的底面直径AB的长.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)过圆柱母线的截面ACEF是正方形,从而截面ACEF⊥平面ABC,AE⊥CF,又AC⊥BC,从而BC⊥截面ACEF,进而BC⊥AE,由此能证明平面ABE⊥平面BCF.
(Ⅱ)平面BEF与平面BCF所成的二面角为60°,设AE∩CF=M,由(Ⅰ)知AE⊥平面BCF,过E作EH⊥BF于H,连接MH,则MH⊥BF,由此能坟出直径AB长.
(Ⅱ)平面BEF与平面BCF所成的二面角为60°,设AE∩CF=M,由(Ⅰ)知AE⊥平面BCF,过E作EH⊥BF于H,连接MH,则MH⊥BF,由此能坟出直径AB长.
解答:
(Ⅰ)证明:∵过圆柱母线的截面ACEF是正方形,
∴截面ACEF⊥平面ABC,AE⊥CF,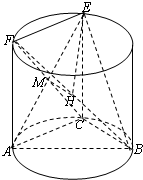
又AB为圆柱底面直径,∴AC⊥BC,
∴BC⊥截面ACEF,∴BC⊥AE,
又∵CF∩BC=C,
∴AE⊥平面BCF,又AE?平面ABE,
∴平面ABE⊥平面BCF.
(Ⅱ)解:平面BEF与平面BCF所成的二面角为60°,
设AE∩CF=M,由(Ⅰ)知AE⊥平面BCF,
过E作EH⊥BF于H,
连接MH,则MH⊥BF,∴∠EHM=60°,
设BC=t,则BE=
,EH=
,
在Rt△EMH中,
依题sin∠EHM=
=
,
∴
=
,
解得t=1,
∴直径AB长为
.
∴截面ACEF⊥平面ABC,AE⊥CF,

又AB为圆柱底面直径,∴AC⊥BC,
∴BC⊥截面ACEF,∴BC⊥AE,
又∵CF∩BC=C,
∴AE⊥平面BCF,又AE?平面ABE,
∴平面ABE⊥平面BCF.
(Ⅱ)解:平面BEF与平面BCF所成的二面角为60°,
设AE∩CF=M,由(Ⅰ)知AE⊥平面BCF,
过E作EH⊥BF于H,
连接MH,则MH⊥BF,∴∠EHM=60°,
设BC=t,则BE=
| t2+1 |
| ||
|
在Rt△EMH中,
依题sin∠EHM=
| ||||||
|
| ||
| 2 |
∴
| ||
|
| ||
|
解得t=1,
∴直径AB长为
| 2 |
点评:本题考查平面与平面垂直的证明,考查直径长的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β<
如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β< 已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点.
已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点. 正△ABC的边长为2,CD是AB边上的高,E,F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).在图(2)中:
正△ABC的边长为2,CD是AB边上的高,E,F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).在图(2)中: 将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)
将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+) 已知函数f(x)=-x2+8x的图象上一点P(1,f(1)),过P作平行于x轴的直线l1,直线l2:x=2,求如图所示的阴影部分的面积S.
已知函数f(x)=-x2+8x的图象上一点P(1,f(1)),过P作平行于x轴的直线l1,直线l2:x=2,求如图所示的阴影部分的面积S.