题目内容
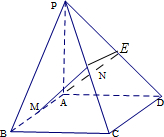
已知PA垂直于矩形ABCD所在平面，M，N分别是AB，PC的中点．（1）求证：CD⊥平面PAD；
（2）求证：MN∥平面PAD．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（1）运用线面垂直的判定定理和性质定理，即可得知；
（2）取PD的中点E，连AE，NE，运用中位线定理，以及线面平行的判定定理，即可得证．
（2）取PD的中点E，连AE，NE，运用中位线定理，以及线面平行的判定定理，即可得证．
解答：
证明：（1）∵PA⊥面ABCD，CD?面ABCD，
∴PA⊥CD，
∵ABCD为矩形，∴CD⊥AD，
又PA∩AD=A，
∴CD⊥平面PAD；
（2）取PD的中点E，连AE，NE，M，N分别是AB，PC的中点，
∵NE∥CD，且NE=CD，
∴AMNE为平行四边形，∴MN∥AE，
又MN?平面PAD，AE?平面PAD，
∴MN∥平面PAD．
证明：（1）∵PA⊥面ABCD，CD?面ABCD，∴PA⊥CD，
∵ABCD为矩形，∴CD⊥AD，
又PA∩AD=A，
∴CD⊥平面PAD；
（2）取PD的中点E，连AE，NE，M，N分别是AB，PC的中点，
∵NE∥CD，且NE=CD，
∴AMNE为平行四边形，∴MN∥AE，
又MN?平面PAD，AE?平面PAD，
∴MN∥平面PAD．
点评：本题考查直线与平面平行、垂直的判定和性质及运用，记熟这些定理是解题的关键，是一道基础题．
练习册系列答案
相关题目
如图，AB为圆柱的底面直径，过母线的截面ACEF是边长为1的正方形，