题目内容
2.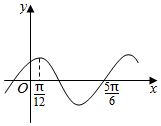 设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )
设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )| A. | f(-$\frac{3π}{4}$)<f($\frac{5π}{3}$)<f($\frac{7π}{6}$) | B. | f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$)<f($\frac{5π}{3}$) | C. | f($\frac{5π}{3}$)<f($\frac{7π}{6}$)<f(-$\frac{3π}{4}$) | D. | f($\frac{5π}{3}$)<f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$) |
分析 根据条件求出函数的周期和对称轴,利用函数周期性,对称性和单调性的关系进行转化比较即可.
解答 解:由图象知$\frac{3T}{4}$=$\frac{5π}{6}-\frac{π}{12}=\frac{3π}{4}$,
则T=π,则函数$\frac{π}{12}+π$=$\frac{13π}{12}$,
$\frac{π}{12}+\frac{π}{2}$=$\frac{7π}{12}$,
则函数在[$\frac{7π}{12}$,$\frac{13π}{12}$]上是增函数,且函数关于x=$\frac{π}{12}$和x=$\frac{7π}{12}$对称,
则f($\frac{5π}{3}$)=f($\frac{5π}{3}$-π)=f($\frac{2π}{3}$),f(-$\frac{3π}{4}$)=f(-$\frac{3π}{4}$+π)=f($\frac{π}{4}$)=f($\frac{11π}{12}$),
f($\frac{7π}{6}$)=f($\frac{π}{6}$)=f(π),
∵$\frac{2π}{3}$<$\frac{11π}{12}$<π,
∴f($\frac{2π}{3}$)<f($\frac{11π}{12}$)<f(π),
即f($\frac{5π}{3}$)<f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$),
故选:D.
点评 本题主要考查函数值的大小比较,根据条件求出函数的周期和对称轴,利用函数周期性,对称性和单调性的关系进行比较是解决本题的关键.

练习册系列答案
相关题目
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位问量,且$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$.向量$\overrightarrow{a}$-$\overrightarrow{c}$与向量$\overrightarrow{b}$-$\overrightarrow{c}$的夹角为$\frac{π}{6}$,则|$\overrightarrow{a}$-$\overrightarrow{c}$|的最大值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2 |
10.已知数列{an}的前n项和Sn=n2+n+1,则:a1+a4=( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
14.已知命题p:?x∈(0,π),x>sinx.则下列说法正确的是( )
| A. | 命题p为假命题;¬p:?x∈(0,π),x>sinx | B. | 命题p为假命题;¬p:?x∈(0,π),x≤sinx | ||
| C. | 命题p为真命题;¬p:?x∈(0,π),x≤sinx | D. | 命题p为真命题;¬p:?x∈(0,π),x≤sinx |
11.函数y=$\frac{3}{2}$cos5x的最大值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{15}{2}$ | D. | 5 |