题目内容
7.在△ABC中,角A,B,C所对的边分别为a,b,c,设A=$\frac{π}{3}$,sinB=3sinC.(1)若a=$\sqrt{7}$,求b的值;
(2)求tanC的值.
分析 (1)由正弦定理化简已知可得:b=3c,利用余弦定理可得7=b2+c2-bc,即可解得b的值.
(2)由三角形内角和定理可得B=$\frac{2π}{3}$-C,从而可得sin($\frac{2π}{3}$-C)=3sinC,利用两角差的正弦函数公式,特殊角的三角函数值,同角三角函数基本关系式即可计算得解tanC的值.
解答 (本题满分为13分)
解:(1)∵sinB=3sinC,
∴由正弦定理可得:b=3c,
∴由余弦定理:a2=b2+c2-2bccosA及A=$\frac{π}{3}$,a=$\sqrt{7}$,可得:7=b2+c2-bc,
∴b2+($\frac{b}{3}$)2-$\frac{{b}^{2}}{3}$=7,解得:b=3…7分
(2)∵A=$\frac{π}{3}$,∴B=$\frac{2π}{3}$-C,
∴sin($\frac{2π}{3}$-C)=3sinC,即:$\frac{\sqrt{3}}{2}$cosC+$\frac{1}{2}$sinC=3sinC,
∴$\frac{\sqrt{3}}{2}$cosC=$\frac{5}{2}$sinC,
∴tanC=$\frac{\sqrt{3}}{5}$…13分
点评 本题主要考查了正弦定理,余弦定理,三角形内角和定理,两角差的正弦函数公式,特殊角的三角函数值,同角三角函数基本关系式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.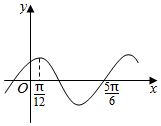 设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )
设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )
 设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )
设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )| A. | f(-$\frac{3π}{4}$)<f($\frac{5π}{3}$)<f($\frac{7π}{6}$) | B. | f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$)<f($\frac{5π}{3}$) | C. | f($\frac{5π}{3}$)<f($\frac{7π}{6}$)<f(-$\frac{3π}{4}$) | D. | f($\frac{5π}{3}$)<f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$) |
12.已知集合A={x|x2-x-2≤0},B={x|x2-1>0},则A∩B=( )
| A. | [-2,1) | B. | (-1,1) | C. | (1,2] | D. | (-2,-1)∪(1,2] |
17.已知函数f(x)=cos(4x-$\frac{π}{3}$)+2cos2(2x),将函数y=f(x)的图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,再将所得函数图象向右平移$\frac{π}{6}$个单位,得到函数y=g(x)的图象,则函数y=g(x)的一个单调递增区间为( )
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{4}$,$\frac{π}{4}$] | C. | [$\frac{π}{6}$,$\frac{2π}{3}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |