题目内容
10．已知数列{an}的前n项和Sn=n2+n+1，则：a1+a4=（ ）| A． | 10 | B． | 11 | C． | 12 | D． | 13 |
分析 由数列的前n项和求得首项，再由a4=S4-S3求得a4，则答案可求．
解答 解：由Sn=n2+n+1，得a1=S1=3，
${a}_{4}={S}_{4}-{S}_{3}={4}^{2}+4+1-（{3}^{2}+3+1）=8$，
∴a1+a4=11．
故选：B．
点评 本题考查数列递推式，训练了利用数列的前n项和求数列中的项，是基础题．
练习册系列答案
口算能手系列答案
相关题目
5．已知函数$y=2sin（2x+φ）（|φ|＜\frac{π}{2}）$的图象经过点（0，-1），则该函数的一个单调递增区间为（ ）
| A． | [-$\frac{π}{6}$，$\frac{π}{3}$] | B． | [$\frac{π}{3}$，$\frac{5π}{6}$] | C． | [-$\frac{5π}{12}$，$\frac{π}{12}$] | D． | [$\frac{π}{12}$，$\frac{7π}{12}$]] |
2．
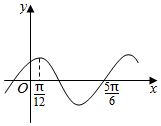设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（ ）
设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（ ）| A． | f（-$\frac{3π}{4}$）＜f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$） | B． | f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$）＜f（$\frac{5π}{3}$） | C． | f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$）＜f（-$\frac{3π}{4}$） | D． | f（$\frac{5π}{3}$）＜f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$） |