题目内容
20.在递增等差数列{an}中,Sn为数列的前项和,S7>7,S9<18,则a8的取值范围是( )| A. | (1,3) | B. | (1,4) | C. | (1,5) | D. | (1,6) |
分析 根据{an}是递增等差数列,S7>7,S9<18,求出a1,d的关系式,利用线性规划求解a8的取值范围.
解答  解:由题意,S7>7,可得a1+a7>2⇒a1+3d>1,
解:由题意,S7>7,可得a1+a7>2⇒a1+3d>1,
S9<18,可得a1+a9<4⇒a1+4d<2,
a8=a1+7d,
作出用a1,d分别表示的横坐标和纵坐标图象,如图已知在点B和点A处使a8取最小值1和最大值5;
故选C.
点评 本题考查了等差数列的通项公式,考查了等差数列的前n项和,线性规划的运用求解最值问题,属于基础题.

练习册系列答案
相关题目
10.设α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),且tanα=$\frac{1}{7}$,tanβ=$\frac{1}{3}$,则α+2β=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
12.要得到函数y=sin2x的图象,只需将函数y=sin(2x-2)的图象上的所有点沿x轴( )
| A. | 向左平移1个单位长度 | B. | 向左平移2个单位长度 | ||
| C. | 向右平移1个单位长度 | D. | 向右平移2个单位长度 |
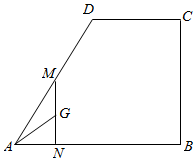 如图,梯形ABCD中,AB=AD=2CD=2,AB||CD,∠DAB=$\frac{π}{3}$,
如图,梯形ABCD中,AB=AD=2CD=2,AB||CD,∠DAB=$\frac{π}{3}$,