题目内容
12．要得到函数y=sin2x的图象，只需将函数y=sin（2x-2）的图象上的所有点沿x轴（ ）| A． | 向左平移1个单位长度 | B． | 向左平移2个单位长度 | ||
| C． | 向右平移1个单位长度 | D． | 向右平移2个单位长度 |
分析 利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．
解答 解：∵y=sin2x=sin[2（x+1）-2]，
∴只需将y=sin（2x-2）的图象向左平移1个单位，即可得到函数y=sin2x的图象．
故选：A．
点评 本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
2．如图是函数f（x）=-x2+ax+b的部分图象，f′（x）是f（x）的导函数，则函数g（x）=ex-f′（x）的零点所在的区间是（ ）
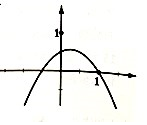
| A． | （-1，-$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，0） | C． | （0，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，1） |
20．在递增等差数列{an}中，Sn为数列的前项和，S7＞7，S9＜18，则a8的取值范围是（ ）
| A． | （1，3） | B． | （1，4） | C． | （1，5） | D． | （1，6） |
7．已知a，b，c 分别是锐角△ABC三个内角A，B，C的对边，且（sin A+sin B）（a-b）=（sin C-sin B ）c，且b+c=8．
（Ⅰ）求A的值；
（Ⅱ） 求△ABC面积的最大值．
（Ⅰ）求A的值；
（Ⅱ） 求△ABC面积的最大值．
17．同时具有性质：①图象的一个零点和其相邻对称轴间的距离是$\frac{π}{4}$；②在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上是增函数的一个函数为（ ）
| A． | y=cos（$\frac{x}{2}$+$\frac{π}{6}$） | B． | y=sin（$\frac{x}{2}$+$\frac{π}{6}$） | C． | y=sin（2x-$\frac{π}{6}$） | D． | y=cos（2x-$\frac{π}{6}$） |
4．若对于任意的实数t，函数f（x）=（x-t）3+（x-et）3-3ax在R上都是增函数，则实数a的取值范围是（ ）
| A． | （-$∞，\frac{1}{2}$] | B． | （$-∞，\frac{1}{2}$） | C． | （$-∞，\frac{\sqrt{2}}{2}$] | D． | （$-∞，\frac{\sqrt{2}}{2}$） |
1．下列函数中，其定义域和值域分别与y=x${\;}^{-\frac{1}{2}}$的定义域和值域相同的是（ ）
| A． | y=|x| | B． | y=3x | ||
| C． | $y={a^{{{log}_a}x}}（a＞0，a≠1）$ | D． | y=lgx |
2．
执行如图所示的程序框图，则输出的s值为（ ）
执行如图所示的程序框图，则输出的s值为（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | 2 | D． | 3 |