题目内容
8.试利用单位圆中的三角函数线证明:当0<α<$\frac{π}{2}$时,sinα<α<tanα.分析 由题意作出三角函数线,进而比较S△AOP,S扇形AOP,S△AOT的大小,可得答案.
解答 证明:在直角坐标系中结合单位圆作出锐角α的正弦线和正切线,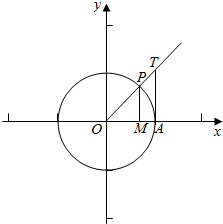
由图可知sinα=MP,α=$\widehat{AP}$,tanα=AT,
∵S△AOP=$\frac{1}{2}$×MP×1=$\frac{1}{2}$sinα,
S扇形AOP=$\frac{1}{2}$×$\widehat{AP}$×1=$\frac{1}{2}$α,
S△AOT=$\frac{1}{2}$×AT×1=$\frac{1}{2}$tanα,
∵S△AOP<S扇形AOP<S△AOT,
∴MP<$\widehat{AP}$<AT,
即sinα<α<tanα,
点评 本题考查单位圆与三角函数线,难度不大,属基础题.

练习册系列答案
相关题目
18.甲、乙两人约好一同去看《变形金刚5》,两人买完了电影票后,偶遇丙也来看这场电影,此时还剩9张该场电影的电影票,电影票的座位信息如表.
丙从这9张电影票中挑选了一张,甲、乙询问丙所选的电影票的座位信息.丙只将排数告诉了甲,只将号数告诉了乙.下面是甲、乙关于丙所选电影票的具体座位信息的一段对话:
甲对乙说:“我不能确定丙的座位信息,你肯定也不能确定.”
乙对甲说:“本来我不能确定,但是现在我能确定了.”
甲对乙说:“哦,那我也能确定了!”
根据上面甲、乙的对话,判断丙选择的电影票是( )
| 1排4号 | 1排5号 | 1排8号 |
| 2排4号 | ||
| 3排1号 | 3排5号 | |
| 4排1号 | 4排2号 | 4排8号 |
甲对乙说:“我不能确定丙的座位信息,你肯定也不能确定.”
乙对甲说:“本来我不能确定,但是现在我能确定了.”
甲对乙说:“哦,那我也能确定了!”
根据上面甲、乙的对话,判断丙选择的电影票是( )
| A. | 4排8号 | B. | 3排1号 | C. | 2排4号 | D. | 1排5号 |
13.不等式x2$-\frac{1}{6}$x$-\frac{1}{6}$<0的解集为( )
| A. | (-$\frac{1}{3}$,$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{2}$,+∞) | C. | (-$\frac{1}{2}$,$\frac{1}{3}$) | D. | (-∞,$-\frac{1}{2}$)∪($\frac{1}{3}$,+∞) |
20.在递增等差数列{an}中,Sn为数列的前项和,S7>7,S9<18,则a8的取值范围是( )
| A. | (1,3) | B. | (1,4) | C. | (1,5) | D. | (1,6) |
17.同时具有性质:①图象的一个零点和其相邻对称轴间的距离是$\frac{π}{4}$;②在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上是增函数的一个函数为( )
| A. | y=cos($\frac{x}{2}$+$\frac{π}{6}$) | B. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | C. | y=sin(2x-$\frac{π}{6}$) | D. | y=cos(2x-$\frac{π}{6}$) |
18.某商品的销售额y(万元)与广告费x(万元)存在线性相关,根据一组样本数据(xi,yi)(i=1,2,3,…,n)用最小二乘法建立的回归方程为y=10+0.4x,则下列结论成立的是( )
| A. | y与x具有负的线性相关关系 | |
| B. | 若r表示变量与之间相关系数,则r=0.4 | |
| C. | 当广告费为1万元时,商品的销售额为10.4万元 | |
| D. | 当广告费为1万元时,商品的销售额为10.4万元左右 |
 某市为提升城市品位,开展植树造林,创建国家森林城市,为了保证树苗的质量,林管部门要在植树前对树苗高度进行抽测,现抽测了6株某种树苗的高度(单位:厘米),得到如图1茎叶图.
某市为提升城市品位,开展植树造林,创建国家森林城市,为了保证树苗的质量,林管部门要在植树前对树苗高度进行抽测,现抽测了6株某种树苗的高度(单位:厘米),得到如图1茎叶图.