Question

17．已知椭圆C_n：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n（a＞b＞0，n∈N^*），F₁、F₂是椭圆C₄的焦点，A（2，$\sqrt{2}$）是椭圆C₄上一点，且$\overrightarrow{A{F}_{2}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0；
（1）求C_n的离心率并求出C₁的方程；
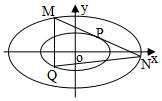
（2）P为椭圆C₂上任意一点，过P且与椭圆C₂相切的直线l与椭圆C₄交于M，N两点，点P关于原点的对称点为Q；求证：△QMN的面积为定值，并求出这个定值．

Answer 1

分析 （1）椭圆C₄的方程为：$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{4{b}^{2}}$=1，由$\overrightarrow{A{F}_{2}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0．∴$\overrightarrow{A{F}_{2}}$⊥$\overrightarrow{{F}_{1}{F}_{2}}$，可得b²，a²即可；
（2）由距离公式得到点P到直线l的距离d，由弦长公式得到MN，△QMN的面积为s=$\frac{1}{2}d•MN$即可得证．

解答 解：（1）椭圆C₄的方程为：C₄：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4    即：$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{4{b}^{2}}$=1
不妨设c²=a²-b²   则F₂（2c，0）
∵$\overrightarrow{A{F}_{2}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0．∴$\overrightarrow{A{F}_{2}}$⊥$\overrightarrow{{F}_{1}{F}_{2}}$，
∴2c=2，$\frac{（2b）^{2}}{2a}$=$\frac{2{b}^{2}}{a}$=$\sqrt{2}$
∴c=1，2b²=$\sqrt{2}$a，2b⁴=a²=b²+1，
∴2b⁴-b²-1=0，
∴（2b²+1）（b²-1）=0，
∴b²=1，a²=2
∴椭圆C_n的方程为：$\frac{{x}^{2}}{2}$+y²=n
∴e²=$\frac{2{n}^{2}-{n}^{2}}{2{n}^{2}}$=$\frac{1}{2}$，∴e=$\frac{\sqrt{2}}{2}$
椭圆C₁的方程为：$\frac{{x}^{2}}{2}$+y²=1；
（2）设P （x₀，y₀），由（1）得C₂：为：$\frac{{x}^{2}}{2}$+y²=2，
∴过P且与椭圆C₂相切的直线l：$\frac{{x}_{0}x}{2}+{y}_{0}y=2$．且x₀²+2y₀²=4
点P关于原点对称点Q （-x₀，-y₀），点Q到直线l的距离d=$\frac{{{x}_{0}}^{2}+2{{y}_{0}}^{2}+4}{\sqrt{{{x}_{0}}^{2}+4{{y}_{0}}^{2}}}=\frac{8}{\sqrt{4+2{{y}_{0}}^{2}}}$
设M（x₁，y₁），N（x₂，y₂）
由.$\left\{\begin{array}{l}{{x}_{0}x+2{y}_{0}y=4}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$得4x²-8x₀x+16-16y₀²=0⇒x²-2x₀x+4-4y₀²=0；
x₁+x₂=2x₀，x₁x₂=4-4y₀²，
MN=$\sqrt{1+\frac{{{x}_{0}}^{2}}{4{{y}_{0}}^{2}}}\sqrt{4{{x}_{0}}^{2}-16+16{{y}_{0}}^{2}}$，
∴△QMN的面积为s=$\frac{1}{2}d•MN=\frac{1}{2}\frac{8}{\sqrt{{{x}_{0}}^{2}+4{{y}_{0}}^{2}}}\sqrt{1+\frac{{{x}_{0}}^{2}}{4{{y}_{0}}^{2}}}\sqrt{4{{x}_{0}}^{2}-16+16{{y}_{0}}^{2}}$=4$\sqrt{2}$（定值）

点评 本题考查了圆锥曲线的定义域几何性质的应用问题，也考查了直线与圆锥曲线的综合应用问题，利用基本不等式求函数的最值问题，是综合性题目．