题目内容
设△ABC的三个内角A,B,C对边分别是a,b,c,若∠A=45°,a=2,b=
.
(1)求∠B的值;
(2)求边c的值.
| 2 |
(1)求∠B的值;
(2)求边c的值.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)由正弦定理可得sinB=
,由大边对大角可得;
(2)由三角形的内角和和三角函数公式可得cosC,代入由余弦定理可得c2=a2+b2-2abcosC,开平方可得答案.
| 1 |
| 2 |
(2)由三角形的内角和和三角函数公式可得cosC,代入由余弦定理可得c2=a2+b2-2abcosC,开平方可得答案.
解答:
解:(1)由题意结合正弦定理可得
sinB=
sinA=
×
=
,
∵b<a,∴B<A,∴B=30°
(2)由三角形的内角和可得C=180°-A-B=105°,
∴cosC=cos105°=cos(60°+45°)
=cos60°cos45°-sin60°sin45°=-
,
由余弦定理可得c2=a2+b2-2abcosC
=6+4
•
=4+2
=(
+1)2,
∴c=
+1
sinB=
| b |
| a |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∵b<a,∴B<A,∴B=30°
(2)由三角形的内角和可得C=180°-A-B=105°,
∴cosC=cos105°=cos(60°+45°)
=cos60°cos45°-sin60°sin45°=-
| ||||
| 4 |
由余弦定理可得c2=a2+b2-2abcosC
=6+4
| 2 |
| ||||
| 4 |
| 3 |
| 3 |
∴c=
| 3 |
点评:本题考查正余弦定理的应用,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
=(
,1),若将向量-2
绕坐标原点逆时针旋转120°得到向量
,则
的坐标为( )
| a |
| 3 |
| a |
| b |
| b |
| A、(0,4) | ||
B、(2
| ||
C、(-2
| ||
D、(2,-2
|

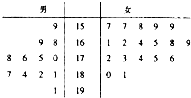 某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)
某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)