题目内容

求下列函数的导数
（1）f（x）=ex•（cosx+sinx）；
（2）f（x）=
2sinx
1+x2
．
考点：导数的运算
专题：导数的概念及应用
分析：根据导数的运算法则即可得到结论．
解答： 解：（1）∵f（x）=ex•（cosx+sinx），
∴f′（x）=ex•（cosx+sinx）+ex•（cosx+sinx）′=ex•（cosx+sinx）+ex•（cosx-sinx）=2ex•cosx；
（2）∵f（x）=
2sinx
1+x2
，∴f′（x）=
2cosx•(1+x2)-2sinx•2x
(1+x2)2
．
点评：本题主要考查导数的基本运算，要求熟练掌握导数的运算法则．
练习册系列答案
相关题目
已知函数f（x）=cos（2x-
π
3
）+2sin（x-
π
4
）sin（x+
π
4
）．
（Ⅰ）求函数f（x）的最小正周期和图象的对称轴方程；
（Ⅱ）求函数f（x）在区间[-
π
12
，
π
2
]上的值域；
（Ⅲ） 令g（x）=f（x-
π
6
），判断函数g（x）的奇偶性，并说明理由．
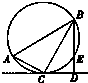如图，在△ABC中，∠ACB=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，求DE的长．
如图为函数，f（x）=Asin（ωx+φ）+k（A＞0，K≠0，ω＞0，|φ|＜
π
2
）的图象的一部分．

（Ⅰ）求f（x）的解析式及f（x）的单调递增区间；
（Ⅱ）求f（1）+f （2）+f（3）+…f（2008）的值．
已知p：-2≤
4-x
3
≤2，q：（x-1-m）（x-1+m）≤0，（m＞0）．￢p是￢q的必要不充分条件，求m的范围．
已设函数f（x）=
ex
x2+ax+a
，其中a为实数．
（Ⅰ）当a=0时，若直线l过（2，0）与f（x）相切，求直线l的方程；
（Ⅱ）若f（x）的定义域为R，求a的取值范围；
（Ⅲ）当f（x）的定义域为R时，求f（x）的单调减区间．
如图，△ABC的外接圆⊙O的半径为5，CE垂直于⊙O所在的平面，BD∥CE，CE=4，BC=6，且BD=1，cos∠ADB=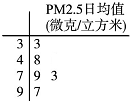
101
101
．
（1）求证：平面AEC⊥平面BCED；
（2）试问线段DE上是否存在点M，使得直线AM与平面ACE所成角的正弦值为
2
21
21
？若存在，确定点M的位置；若不存在，请说明理由．
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．我国PM2.5标准采用世卫组织设定的最宽限值，PM2.5日均值在35微克/立方米以下空气质量为一级；在35～75微克/立方米之间空气质量为二级；在75微克/立方米及其以上空气质量为超标．某试点城市环保局从该市市区2012年全年每天的PM2.5监测数据中随机抽取5天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶），若从这5天的数据中随机抽出2天．
（1）求恰有一天空气质量超标的概率；
（2）求至多有一天空气质量超标的概率．
已知圆C过点（-1，0），且圆心在x轴的负半轴上，直线l：y=x+1被该圆所截得的弦长为2
2
，则圆C的标准方程为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网