题目内容
在△ABC中,若AC⊥BC,BC=a,AC=b,则△ABC的外接圆半径为r=
,将此结论类比到空间,可得到正确的结论:在四面体S-ABC中,若SA,SB,SC两两垂直,SA=a,SB=b,SC=c,则四面体S-ABC的外接球半径为R= .
| ||
| 2 |
考点:类比推理
专题:规律型,推理和证明
分析:可将图形补成以SA,SB,SC为相邻的边的长方体,运用长方体的对角线即为外接球的直径,即可得出结论.
解答:
解:由平面图形的性质类比推理空间图形的性质时
一般是由点的性质类比推理到线的性质,
由线的性质类比推理到面的性质,
由圆的性质推理到球的性质.
由已知在平面几何中,△ABC中,若AB⊥AC,AC=b,BC=a,
则△ABC的外接圆半径r=
,
我们可以类比这一性质,推理出:
在四面体S-ABC中,若SA、SB、SC两两垂直,SA=a,SB=b,SC=c,
则构造以S为顶点,SA,SB,SC为长方体的相邻的三条棱,其外接球的直径为长方体的对角线,可得四面体S-ABC的外接球半径R=
.
故答案为:
.
一般是由点的性质类比推理到线的性质,
由线的性质类比推理到面的性质,
由圆的性质推理到球的性质.
由已知在平面几何中,△ABC中,若AB⊥AC,AC=b,BC=a,
则△ABC的外接圆半径r=
| ||
| 2 |
我们可以类比这一性质,推理出:
在四面体S-ABC中,若SA、SB、SC两两垂直,SA=a,SB=b,SC=c,
则构造以S为顶点,SA,SB,SC为长方体的相邻的三条棱,其外接球的直径为长方体的对角线,可得四面体S-ABC的外接球半径R=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:由平面图形的性质类比推理空间图形的性质时,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由圆的性质推理到球的性质.

练习册系列答案
相关题目
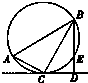 如图,在△ABC中,∠ACB=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,求DE的长.
如图,在△ABC中,∠ACB=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,求DE的长. 如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,cos∠ADB=
如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,cos∠ADB=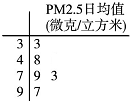 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.某试点城市环保局从该市市区2012年全年每天的PM2.5监测数据中随机抽取5天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这5天的数据中随机抽出2天.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.某试点城市环保局从该市市区2012年全年每天的PM2.5监测数据中随机抽取5天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这5天的数据中随机抽出2天.