题目内容
1.已知f(x)=|x|-1,关于x的方程f2(x)-|f(x)|+k=0,则下列四个结论错误的是( )| A. | 存在实数k,使方程恰有2个不同的实根 | |
| B. | 存在实数k,使方程恰有3个不同的实根 | |
| C. | 存在实数k,使方程恰有5个不同的实根 | |
| D. | 存在实数k,使方程恰有8个不同的实根 |
分析 化简f(x)=|x|-1≥-1,再令f(x)=t,从而化方程f2(x)-|f(x)|+k=0为k=|t|-t2,从而作函数k=|t|-t2的图象,结合图象分类讨论解得.
解答 解:∵f(x)=|x|-1≥-1,
∴当a=-1时,f(x)=a有且只有一个解,
当a>-1时,f(x)=a有两个不同的解,
∵令f(x)=t,则方程f2(x)-|f(x)|+k=0可化为k=|t|-t2,
作函数k=|t|-t2的图象如下,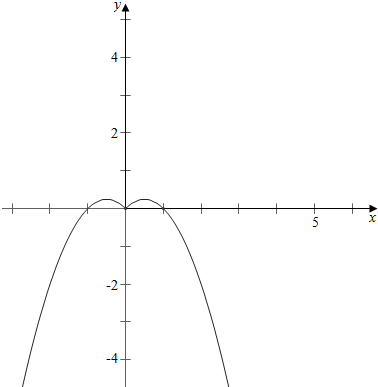 ,
,
结合图象可知,
当k=$\frac{1}{4}$时,k=|t|-t2有两个不同的解,且t=±$\frac{1}{2}$,
故方程方程f2(x)-|f(x)|+k=0有四个不同的解,
当0<k<$\frac{1}{4}$时,k=|t|-t2有4个不同的解,且-1<t<1,
故方程方程f2(x)-|f(x)|+k=0有8个不同的解;
当k=0时,k=|t|-t2有三个不同的解,分别为-1,0,1;
故方程方程f2(x)-|f(x)|+k=0有5个不同的解,
当k<0时,k=|t|-t2有两个不同的解,且t<-1或t>1,
故方程方程f2(x)-|f(x)|+k=0有2个不同的解;
故选B.
点评 本题考查了分类讨论与数形结合的思想应用,同时考查了函数的零点与方程的根的关系应用.

练习册系列答案
相关题目
12.三次函数f(x)=x3-3x+1的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.设全集U=R,集合A={x|1<2x<4},B={x|log2x>0},则(∁UA)∩B=( )
| A. | [2,+∞) | B. | (1,2] | C. | (-∞,0]∪[2,+∞) | D. | (-∞,0]∪(1,+∞) |
13.定义在R的奇函数f(x),当x<0时,f(x)=-x2+x,则f(2)等于( )
| A. | 4 | B. | 6 | C. | -4 | D. | -6 |