题目内容
6.设函数f(x)=-x2+2x+a(0≤x≤3,a≠0)的最大值为m,最小值为n.(1)求m,n的值(用a表示);
(2)若角θ的终边经过点P(m-1,n+3),求$\frac{{2sin(θ-π)+sin(\frac{3π}{2}+θ)}}{{cos(-θ)+cos(\frac{5π}{2}-θ)}}$的值.
分析 (1)由条件利用二次函数的性质,求得m、n的值.
(2)由条件利用任意角的三角函数的定义求得tanα的值,再同角三角函数的基本关系,求得所给式子的值.
解答 解:(1)根据函数f(x)=-x2+2x+a(0≤x≤3,a≠0),
可得f(x)=-(x-1)2+1+a,而0≤x≤3,
∴m=f(1)=1+a,n=f(3)=-3+a.
(2)由(1)知角θ的终边经过点P(a,a),∴tanθ=1,所以cosθ≠0,
原式=$\frac{-2sinθ-cosθ}{cosθ+sinθ}$=$\frac{-2tanθ-1}{1+tanθ}=-\frac{3}{2}$.
点评 本题主要考查二次函数的性质,任意角的三角函数的定义,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
1.已知f(x)=|x|-1,关于x的方程f2(x)-|f(x)|+k=0,则下列四个结论错误的是( )
| A. | 存在实数k,使方程恰有2个不同的实根 | |
| B. | 存在实数k,使方程恰有3个不同的实根 | |
| C. | 存在实数k,使方程恰有5个不同的实根 | |
| D. | 存在实数k,使方程恰有8个不同的实根 |
11.球O半径为R=13,球面上有三点A、B、C,AB=12$\sqrt{3}$,AC=BC=12,则四面体OABC的体积是( )
| A. | 60$\sqrt{3}$ | B. | 50$\sqrt{3}$ | C. | 60$\sqrt{6}$ | D. | 50$\sqrt{6}$ |
18.已知f(x)=2x+1,则f(2)=( )
| A. | 5 | B. | 0 | C. | 1 | D. | 2 |
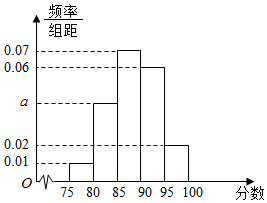 某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].
某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].