题目内容
已知椭圆C:
+y2=1.
(1)求椭圆C截直线l1:y=
(x+1)所得的弦长;
(2)直线l2交椭圆C于M、N两点,椭圆与y轴的正半轴交于B点,若△BMN的重心恰好落在椭圆的右焦点上,判断l2是否存在,若存在求出,不存在说明理由?
| x2 |
| 2 |
(1)求椭圆C截直线l1:y=
| 2 |
(2)直线l2交椭圆C于M、N两点,椭圆与y轴的正半轴交于B点,若△BMN的重心恰好落在椭圆的右焦点上,判断l2是否存在,若存在求出,不存在说明理由?
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)设A(x1,y1),B(x2,y2).直线方程与椭圆的方程联立可得5x2+8x+2=0,可得根与系数的关系,利用弦长公式|AB|=
即可得出.
(2)设MN的中点为P(s,t),假设△BMN的重心恰好落在椭圆的右焦点F(1,0)上,利用
=2
,解得P(
,-
).即可判断出.
| (1+2)[(x1+x2)2-4x1x2] |
(2)设MN的中点为P(s,t),假设△BMN的重心恰好落在椭圆的右焦点F(1,0)上,利用
| BF |
| FP |
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)设A(x1,y1),B(x2,y2).
联立
,化为5x2+8x+2=0,
∴x1+x2=-
,x1x2=
.
∴|AB|=
=
=
.
(2)设MN的中点为P(s,t),
假设△BMN的重心恰好落在椭圆的右焦点F(1,0)上,
则
=2
,解得P(
,-
).
而
>
=a,
弦MN的中点横坐标>a,在椭圆的外部,因此直线MN不可能存在.
联立
|
∴x1+x2=-
| 8 |
| 5 |
| 2 |
| 5 |
∴|AB|=
| (1+2)[(x1+x2)2-4x1x2] |
3×[(
|
6
| ||
| 5 |
(2)设MN的中点为P(s,t),
假设△BMN的重心恰好落在椭圆的右焦点F(1,0)上,
则
| BF |
| FP |
| 3 |
| 2 |
| 1 |
| 2 |
而
| 3 |
| 2 |
| 2 |
弦MN的中点横坐标>a,在椭圆的外部,因此直线MN不可能存在.
点评:本题考查了直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、中点弦问题、三角形的重心的性质、向量运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知函数f(x)=
-logax的零点为x1,函数g(x)=
-ax的正零点为x2,其中a>0且a≠1,m>1,则下列选项一定正确的是( )
| m-x2 |
| m-x2 |
| A、x12+x22=m |
| B、x1>x2 |
| C、x1<x2 |
| D、x12+x22的值与a值有关 |
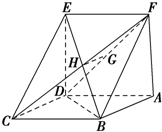 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.四棱锥F-ABCD的体积的最大值( )
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.四棱锥F-ABCD的体积的最大值( )