��Ŀ����
������R�ϵĺ���g(x)�����κ���h(x)���㣺g(x)��2g(��x)��ex��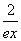 ��9��h(��2)��h(0)��1��h(��3)����2.
��9��h(��2)��h(0)��1��h(��3)����2.
(1)��g(x)��h(x)�Ľ���ʽ��
(2)����x1��x2��[��1,1]������h(x1)��ax1��5��g(x2)��x2g(x2)��������a��ȡֵ��Χ��
(3)��f(x)��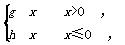 ��(2)�������£����۷���f[f(x)]��a��5�Ľ�ĸ��������
��(2)�������£����۷���f[f(x)]��a��5�Ľ�ĸ��������
�⣺(1)��g(x)��2g(��x)��ex��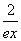 ��9����
��9����
��g(��x)��2g(x)��e��x��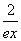 ��9����g(��x)��2g(x)��2ex��
��9����g(��x)��2g(x)��2ex�� ��9����
��9����
�ɢ٢�������ã�g(x)��ex��3.
��h(x)�Ƕ��κ�������h(��2)��h(0)��1������h(x)��ax(x��2)��1��
��h(��3)����2�����a����1��
��h(x)����x(x��2)��1����x2��2x��1��
��g(x)��ex��3��h(x)����x2��2x��1.
(2)����(x)��h(x)��ax��5����x2��(a��2)x��6��
F(x)��g(x)��xg(x)��ex��3��x(ex��3)��(1��x)ex��3x��3��
������֪������1��x��1ʱ����(x)min��F(x)max.
��F��(x)����ex��(1��x)ex��3����xex��3����[��1,1]�ϵ����ݼ���
��F��(x)min��F��(1)��3��e>0��
��F(x)��[��1,1]�ϵ�����������F(x)max��F(1)��0��
�� ��ã�3��a��7��
��ã�3��a��7��
��ʵ��a��ȡֵ��ΧΪ[��3,7]��
(3)��t��a��5����(2)֪��2��t��12.
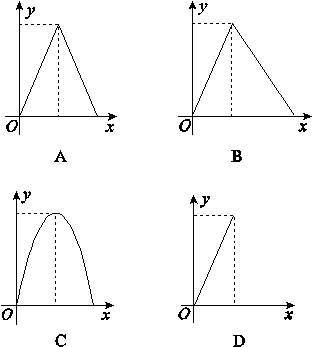
f(x)��ͼ����ͼ��ʾ��

��f(x)��T����f(T)��t.
��t��2����a����3ʱ��T����1����T��ln 5��f(x)����1��2���⣬f(x)��ln 5��3���⣻
��2<t<e2��3������3<a<e2��8ʱ��T��ln(t��3)��ln 5<T<2��f(x)��T��3���⣻
��t��e2��3����a��e2��8ʱ��T��2��f(x)��T��2���⣻
��e2��3<t��12����e2��8<a��7ʱ��T��ln(t��3)>2��f(x)��T��1���⣮
����������
��a����3ʱ��������5���⣻
����3<a<e2��8ʱ��������3���⣻
��a��e2��8ʱ��������2���⣻
��e2��8<a��7ʱ��������1���⣮

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д� �У���
���� ��
�� ��
�� �ĶԱ߷ֱ���a��b��c����֪
�ĶԱ߷ֱ���a��b��c����֪ ����
���� �� �� ��
�� �� �� B. 16
B. 16 C. 9
C. 9
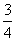 B.
B.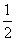 <a<
<a<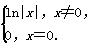 ���Ϻ����ǡ�H���������������Ϊ________��
���Ϻ����ǡ�H���������������Ϊ________��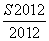 ��
�� ��2 002����S2 014��ֵ����(����)
��2 002����S2 014��ֵ����(����)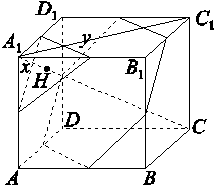
 �����BC��ֵΪ(����)
�����BC��ֵΪ(����)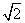 B.
B.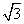 C.
C.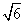 D��6
D��6