题目内容
14.函数$f(x)=2cos({ωx+\frac{π}{3}})$(ω>0)的最小正周期为π.(1)求ω的值;
(2)记△A BC内角 A,B,C的对边分别为a,b,c,若$f({\frac{A}{2}-\frac{π}{6}})=1$,且$a=\frac{{\sqrt{3}}}{2}b$,求sin B的值.
分析 (1)由T=$\frac{2π}{ω}$=π,得ω=2
(2)由(1)可知,f($\frac{A}{2}-\frac{π}{6}$)=2cosA=1,得$cosA=\frac{1}{2}$,$sinA=\frac{\sqrt{3}}{2}$,又$a=\frac{{\sqrt{3}}}{2}b$,且$\frac{a}{sinA}=\frac{b}{sinB}$,可得sinB=$\frac{bsinA}{a}$.
解答 解:(1)∵T=$\frac{2π}{ω}$=π,∴ω=2
(2)由(1)可知,f($\frac{A}{2}-\frac{π}{6}$)=2cosA=1,
∴$cosA=\frac{1}{2}$
∵0<A<π,∴$sinA=\frac{\sqrt{3}}{2}$
又$a=\frac{{\sqrt{3}}}{2}b$,且$\frac{a}{sinA}=\frac{b}{sinB}$,
所以sinB=$\frac{bsinA}{a}$=$\frac{2}{\sqrt{3}}×\frac{\sqrt{3}}{2}=1$
点评 本题考查了三角函数的性质,正弦定理的应用,属于中档题.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 若直线l1与l2斜率相等,则l1∥l2 | |
| B. | 若直线l1∥l2,则k1=k2 | |
| C. | 若直线l1,l2的斜率不存在,则l1∥l2 | |
| D. | 若两条直线的斜率不相等,则两直线不平行 |
19.已知函数f(x)=$\left\{\begin{array}{l}{sin\frac{π}{2}x-1,x<0}\\{lo{g}_{a}x,x>0}\end{array}\right.$(a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | ($\frac{\sqrt{3}}{5}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
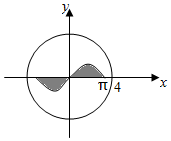 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.