题目内容
16.已知直线$l:\sqrt{3}x+y-2\sqrt{3}=0$与圆C:x2+y2=4相交于A,B两点.(1)求|AB|;
(2)求弦AB所对圆心角的大小.
分析 (1)联立方程组,求出A,B的坐标,由此能求出|AB|.
(2)由|AB|=|OB|=|OA|=2,得△AOB是等边三角形,由此能求出弦AB所对圆心角的大小.
解答 解:(1)如图所示,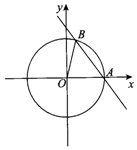
由$\left\{\begin{array}{l}\sqrt{3}x+y-2\sqrt{3}=0\\{x^2}+{y^2}=4\end{array}\right.$,消去y,得x2-3x+2=0,
解得x1=2,x2=1,∴$A(2,0),B(1,\sqrt{3})$,
∴$|AB|=\sqrt{{{(2-1)}^2}+{{(0-\sqrt{3})}^2}}=2$.
(2)又∵|OB|=|OA|=2,
∴△AOB是等边三角形,
∴$∠AOB=\frac{π}{3}•$
点评 本题考查弦长的求法,考查弦所对的圆心角的求法,考查圆、直线方程、两点间距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设y=f(x)为定义在R上的可导函数,定义运算⊕和?如下:对任意m,n∈R均有m⊕n=|f(m)|•n;m?n=f'(m)+n.若存在a∈R,使得对于任意x∈R,恒有a⊕x=a?x=x成立,则称实数a为函数的基元,则下列函数中恰有两个基元的是( )
| A. | f(x)=x2+1 | B. | $f(x)=\frac{1}{2}({x^3}-3x)$ | C. | f(x)=2x3+3x2 | D. | f(x)=cosx |
1.$\int_1^2{\frac{2}{x}}dx$=( )
| A. | 2ln2 | B. | -2ln2 | C. | ln2 | D. | -ln2 |
8.已知曲线C满足方程$\left\{\begin{array}{l}{x=t}\\{y=\sqrt{2t-1}}\end{array}\right.$(t为参数),则曲线C上点的横坐标的取值范围是( )
| A. | R | B. | [0,+∞) | C. | [1,+∞) | D. | [$\frac{1}{2}$,+∞) |
5.从点(2,3)射出的光线沿斜率k=$\frac{1}{2}$的方向射到y轴上,则反射光线所在的直线方程为( )
| A. | x+2y-4=0 | B. | 2x+y-1=0 | C. | x+6y-16=0 | D. | 6x+y-8=0 |
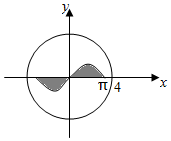 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.