题目内容
已知函数f(x)的导函数为f′(x),且满足f(x)=x3-x•f′(2),则函数f(x)在点(2,f(2))处的切线方程为 .
考点:导数的运算,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:f(x)=x3-x•f′(2),可得f′(x)=3x2-f′(2),令x=2,可得f′(2)=6.可得f(x),利用点斜式即可得出切线方程.
解答:
解:∵f(x)=x3-x•f′(2),
∴f′(x)=3x2-f′(2),
令x=2,可得f′(2)=6.
∴f(x)=x3-6x,
∴f(2)=23-6×2=-4.
∴函数f(x)在点(2,f(2))处的切线方程为y-(-4)=6(x-2),
化为6x-y-16=0,
故答案为:6x-y-16=0.
∴f′(x)=3x2-f′(2),
令x=2,可得f′(2)=6.
∴f(x)=x3-6x,
∴f(2)=23-6×2=-4.
∴函数f(x)在点(2,f(2))处的切线方程为y-(-4)=6(x-2),
化为6x-y-16=0,
故答案为:6x-y-16=0.
点评:本题考查了导数的几何意义、切线方程、点斜式,属于基础题.

练习册系列答案
相关题目
函数y=|log
x|的定义域为[m,n](m<n),值域为[0,1],则n-m的最小值为( )
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中正确的是( )
| A、命题“若x>y,则-x<-y”的逆命题是“若-x>-y,则x<y” |
| B、若命题P:?x∈R,x2+1>0,则¬P:?x∈R,x2+1>0 |
| C、设l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β |
| D、设x,y∈R,则“(x-y)•x2<0”是“x<y”的必要而不充分条件 |
已知cos(
+φ)=-
,且角φ的终边上有一点(2,a)则a=( )
| π |
| 2 |
| ||
| 2 |
A、-
| ||
B、2
| ||
C、±2
| ||
D、
|
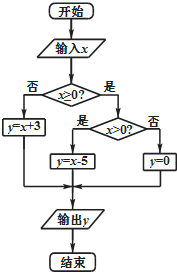 执行如图所示的程序框图,在集合A={x∈R|-10≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间(-5,3)内的概率为( )
执行如图所示的程序框图,在集合A={x∈R|-10≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间(-5,3)内的概率为( )