题目内容
17．已知$\overrightarrow a=（2，4），\overrightarrow b=（x，-2），且\overrightarrow a∥\overrightarrow b$，则x=-1．分析 利用向量共线定理即可得出．
解答 解：∵$\overrightarrow{a}∥\overrightarrow{b}$，∴4x+4=0，解得x=-1．
故答案为：-1．
点评 本题考查了向量共线定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
应用题作业本系列答案
相关题目
7．
为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800名学生参加了这次竞赛，为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，得到如下的频率分布表：
请你根据频率分布表解答下列问题：
（1）求出频率分布表中①、②、③、④、⑤处的值；
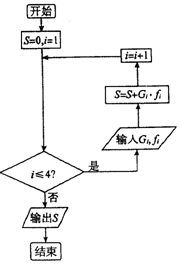
（2）在上述统计数据的分析中，有一项指标计算的程序框图如图所示，则该程序功能是什么？求输出S的值．
为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800名学生参加了这次竞赛，为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，得到如下的频率分布表：| 序号 （i） | 分组 （分数） | 组中值 （Gi） | 频数 （人数） | 频率 （Fi） |
| 1 | [60，70） | 65 | ① | 0.10 |
| 2 | [70，80） | 75 | 20 | ② |
| 3 | [80，90） | 85 | ③ | 0.20 |
| 4 | [90，100） | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
（1）求出频率分布表中①、②、③、④、⑤处的值；
（2）在上述统计数据的分析中，有一项指标计算的程序框图如图所示，则该程序功能是什么？求输出S的值．
8．若f（x）在R上可导，$f（x）={x^2}+2f'（\frac{π}{2}）x+sin2x$，则$\int_0^1{f（x）dx}$=（ ）
| A． | $\frac{7}{3}-π-cos2$ | B． | $\frac{11}{6}-π+\frac{1}{2}cos2$ | C． | $\frac{17}{6}-π-\frac{1}{2}cos2$ | D． | $\frac{11}{6}-π-\frac{1}{2}cos2$ |
12．△ABC中，角A、B、C所对的边分别是a、b、c，若a=2，b=3，$c=\sqrt{5}$，则cosC=（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |