题目内容
1.设等比数列{an}满足a1+a3=20,a2+a4=10,则a1a2a3..an的最大值为210.分析 利用等比数列的通项公式可得:an.指数运算性质、二次函数的单调性即可得出.
解答 解:设等比数列{an}的公比为q,∵a1+a3=20,a2+a4=10,
∴$\left\{\begin{array}{l}{{a}_{1}(1+{q}^{2})=20}\\{{a}_{1}(q+{q}^{3})=10}\end{array}\right.$,解得a1=16,q=$\frac{1}{2}$.
∴an=$16×(\frac{1}{2})^{n-1}$=25-n.
则a1a2a3..an=24+3+…+(5-n)=${2}^{\frac{n(4+5-n)}{2}}$=${2}^{-\frac{1}{2}(n-\frac{9}{2})^{2}+\frac{81}{8}}$,
当且仅当n=4或5时,a1a2a3..an的最大值为210.
故答案为:210.
点评 本题考查了等比数列的通项公式、指数运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(0≤x≤1)}\\{f(x-1)+m(x>1)}\end{array}\right.$在定义域[0,+∞)上单调递增,且对于任意a≥0,方程f(x)=a有且只有一个实数解,则函数g(x)=f(x)-x在区间[0,2n](n∈N*)上所有零点的和为( )
| A. | $\frac{n(n+1)}{2}$ | B. | 22n-1+2n-1 | C. | $\frac{(1+{2}^{n})^{2}}{2}$ | D. | 2n-1 |
11.椭圆$\frac{x^2}{m}+\frac{y^2}{4}=1$的焦距为$2\sqrt{2}$,则m的值等于( )
| A. | 5或-3 | B. | 2或6 | C. | 5或3 | D. | $\sqrt{5}$或$\sqrt{3}$ |
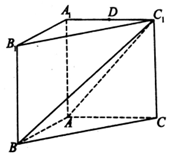 如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C
如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C