题目内容

若loga2=m，loga3=π，其中a＞0，且a≠1，则am+n=
 
．
考点：指数式与对数式的互化,对数的运算性质
专题：函数的性质及应用
分析：通过对数式与指数式的互化，利用指数的运算法则求解即可．
解答： 解：loga2=m，可得：am=2
loga3=π，an=3．
am+n=aman=3×2=6．
故答案为：6．
点评：本题考查指数式与对数式的互化，指数的运算法则，基本知识的考查．
练习册系列答案
相关题目
设
a
=（cosα，（λ-1）sinα），
b
=（cosβ，sinβ），（λ＞0，0＜α＜β＜
π
2
）是平面上的两个向量，若向量
a
+
b
与
a
-
b
互相垂直．
（1）求实数λ的值；
（2）若
a
•
b
=
4
5
，且tanβ=
4
3
，求tan（α-
π
4
）的值．
三个数字log47，log 
1
2
3，2 
2
按从大到小的顺序排列为
 
．
已知函数y=Asin（ωx+φ）+b（A＞0，ω＞0，|φ|＜
π
2
）在一个周期内的图象如图所示，则此函数的解析式为
 
．
已知函数y=f（x）的图象在点M（1，f（1））处的切线方程是y=x+3，则f（1）+f′（1）=
 
．
已知p：
5
x+1
≥1，q：x2-2x+1-m2＜0（m＞0），若p是q的必要不充分条件，则实数m的取值范围是
 
．
已知命题p：无穷数列{an}的前n项和为Sn，若{an}是等差数列，则点（n，Sn）在同一条抛物线上；命题q：若实数m＞1，则mx2+2（m-2）x+1＞0的解集为R，对于命题p的逆否命题s与命题q的逆命题r，下列判断正确的是（　　）
A、s是假命题，r是真命题
B、s是真命题，r假命题
C、s是假命题，r是假命题
D、s是真命题，r是真命题
等差数列{an}中，已知a1=3，a3+a6=7，则a8等于（　　）
A、4B、5C、6D、7
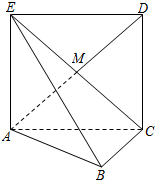如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．
（1）求证：AM⊥平面EBC；
（2）当AC=2时，求三棱锥V E-ABM的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网