题目内容
18.已知sinαcosβ=$\frac{1}{4}$,则cosαsinβ的取值范围[-$\frac{3}{4}$,$\frac{3}{4}$].分析 利用两角和差的正弦公式建立不等式关系进行求解即可.
解答 解:∵sinαcosβ=$\frac{1}{4}$,
∴sin(α+β)=sinαcosβ+cosαsinβ=$\frac{1}{4}$+sinβcosα
sin(α-β)=sinαcosβ-cosαsinβ=$\frac{1}{4}$-sinβcosα
∵-1≤sin(α+β)≤1,-1≤sin(α-β)≤1.
∴-1≤$\frac{1}{4}$+sinβcosα≤1,-1≤$\frac{1}{4}$-sinβcosα≤1,
即--$\frac{5}{4}$≤sinβcosα≤$\frac{3}{4}$,且-$\frac{3}{4}$≤sinβcosα≤$\frac{5}{4}$,
综上-$\frac{3}{4}$≤sinβcosα≤$\frac{3}{4}$,
故答案为:[-$\frac{3}{4}$,$\frac{3}{4}$].
点评 本题考查三角函数值的取值范围,利用两角和与差的正弦公式是解决本题的关键.,解题时要认真审题,仔细解答,注意三角函数的恒等变换.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.将函数f(x)=$\sqrt{3}$sin(ωx-$\frac{π}{3}$)的图象分别向左和向右移动$\frac{π}{3}$之后的图象的对称中心重合,则正实数ω的最小值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{3}$ |
6.有一个质地均匀的四面体玩具,四个面分别标注了数字1、2、3、4,甲、乙两位学生进行如下游戏:甲先抛掷一次,记下四面体朝下的数字为,再由乙抛掷一次,朝下数字为b,若|a-b|≤1就称甲乙两人“默契配合”,则甲、乙两人“默契配合”的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
13.数据a1,a2,a3,a4,a5的方差为10,平均数为3,则数据2a1-1,2a2-1,2a3-1,2a4-1,2a5-1的标准差和平均数分别是( )
| A. | 2$\sqrt{10}$,5 | B. | 40,5 | C. | 2$\sqrt{10}$,3 | D. | 40,4 |
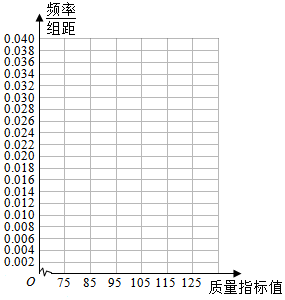
3.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得到如下频数分布表.
(1)作出这些数据的频率分布直方图(用阴影表示);
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计这种产品质量指标值的平均数$\overline{x}$及方差s2;
(3)当质量指标值位于(79.6,120.4)时,认为该产品为合格品.由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline{x}$,σ2近似为样本方差s2(每组数取中间值).
①利用该正态分布,求从该厂生产的产品中任取一件,该产品为合格品的概率;
②该企业每年生产这种产品10万件,生产一件合格品利润10元,生产一件不合格品亏损20元,则该企业的年利润是多少?
(提示:$\sqrt{104}$≈10.2,若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,P(μ-2σ<Z<μ+2σ)=0.9544)
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
| 频数 | 6 | 26 | x | 22 | 8 |

(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计这种产品质量指标值的平均数$\overline{x}$及方差s2;
(3)当质量指标值位于(79.6,120.4)时,认为该产品为合格品.由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline{x}$,σ2近似为样本方差s2(每组数取中间值).
①利用该正态分布,求从该厂生产的产品中任取一件,该产品为合格品的概率;
②该企业每年生产这种产品10万件,生产一件合格品利润10元,生产一件不合格品亏损20元,则该企业的年利润是多少?
(提示:$\sqrt{104}$≈10.2,若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,P(μ-2σ<Z<μ+2σ)=0.9544)
10.设数列{an}和{bn}分别是等差数列与等比数列,且a1=b1=9,a7=b7=1,则以下结论正确的是( )
| A. | a3<a4 | B. | a4>b4 | C. | a4<b4 | D. | b3<b4 |
7.已知数列{an}的前n项和Sn=1-3+5-7+…+(-1)n-1(2n-1)(n∈N*),则S17+S23+S50=( )
| A. | 90 | B. | 10 | C. | -10 | D. | 22 |
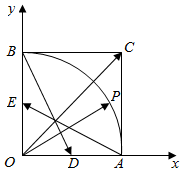 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )