题目内容
9.已知$\overrightarrow{m}$=($\sqrt{3}$sinx,2),$\overrightarrow{n}$=(2cosx,cos2x),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$,(1)求函数f(x)的值域;
(2)在△ABC中,角A,B,C和边a,b,c满足a=2,f(A)=2,sinB=2sinC,求边c.
分析 (1)根据向量的坐标运算以及二倍角公式,化简求出f(x),根据三角函数的性质求出值域;
(2)先求出A的大小,再根据正弦余弦定理即可求出.
解答 解:(1)∵$\overrightarrow{m}$=($\sqrt{3}$sinx,2),$\overrightarrow{n}$=(2cosx,cos2x),
∴f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=2$\sqrt{3}$sinxcosx+2cos2x=$\sqrt{3}$sin2x+cos2x+1=2sin(2x+$\frac{π}{6}$)+1,
∵-1≤sin(2x+$\frac{π}{6}$)≤1,
∴-1≤2sin(2x+$\frac{π}{6}$)+1≤3,
∴函数f(x)的值域为[-1,3];
(2)∵f(A)=2,
∴2sin(2A+$\frac{π}{6}$)+1=2,
∴sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$
∴2A+$\frac{π}{6}$=2kπ+$\frac{π}{6}$,或2A+$\frac{π}{6}$=2kπ+$\frac{5π}{6}$,k∈Z,
∴A=kπ,(舍去),A=kπ+$\frac{π}{3}$,k∈Z,
∵0<A<π,
∴A=$\frac{π}{3}$,
∵sinB=2sinC,由正弦定理可得b=2c,
∵a=2,由余弦定理可得,a2=b2+c2-2bccosA,
∴3c2=4,
解得c=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了向量的数量积德运算,三角函数的化简求值,正弦余弦定理,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.已知菱形ABCD的边长为为4,∠ABC=$\frac{π}{3}$,向其内部随机投放一点P,则点P与菱形各顶点距离均大于1的概率为( )
| A. | 1-$\frac{\sqrt{3}π}{24}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{24}$ | D. | $\frac{\sqrt{3}π}{12}$ |
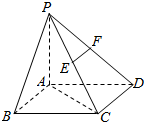 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.