题目内容
5.若复数z0=i在复平面上所对应的点为Z0,动点Z所对应的复数为z,且|z|=2,则|ZZ0|的取值范围为[1,3].分析 点Z的轨迹是以原点为圆心,以2为半径的圆,根据圆的几何性质得出|ZZ0|的最大值和最小值.
解答 解:∵|z|=2,∴点Z的轨迹是以原点为圆心,以2为半径的圆,作出复平面如图:
由图形可知当z=2i时,|ZZ0|取得最小值1,当z=-2i时,|ZZ0|取得最大值3.
故答案为[1,3].
点评 本题考查了复数与复平面的点的对应关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如图是一个几何体的三视图,则该几何体的体积为( )


| A. | $\frac{80}{3}$ | B. | $\frac{70}{3}$ | C. | 23 | D. | 24 |
16.在平面直角坐标系xOy中,若曲线y=2x2+$\frac{a}{x}$(a是常数)过点P(-1,-30),则函数y=2x2+$\frac{a}{x}$在区间[1,4]的最大值与最小值的和为64.
17.已知菱形ABCD的边长为为4,∠ABC=$\frac{π}{3}$,向其内部随机投放一点P,则点P与菱形各顶点距离均大于1的概率为( )
| A. | 1-$\frac{\sqrt{3}π}{24}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{24}$ | D. | $\frac{\sqrt{3}π}{12}$ |
15.已知函数f(x)=sin(ωx-$\frac{π}{6}$)(ω>0),x∈R.,f(α)=-1,f(β)=0,若|α-β|的最小值为$\frac{3π}{4}$,则函数f(x)的单调递增区间为( )
| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5}{2}$π+2kπ],k∈Z | D. | [π+3kπ,$\frac{5}{2}$π+3kπ],k∈Z |
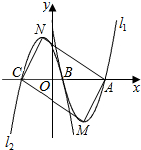 如图,己知抛物线11:y=x2-8x+12与x轴分别交于A、B两点,顶点为M.将抛物线11关于x轴作轴对称变换后再向左平移得到抛物线12,若抛物线12过点B,与x轴的另一个交点为C,顶点为N,则四边形AMCN的面积为32.
如图,己知抛物线11:y=x2-8x+12与x轴分别交于A、B两点,顶点为M.将抛物线11关于x轴作轴对称变换后再向左平移得到抛物线12,若抛物线12过点B,与x轴的另一个交点为C,顶点为N,则四边形AMCN的面积为32.