题目内容
20.已知直线$\sqrt{3}$x-y-$\sqrt{3}$=0与x轴的交点为N,与抛物线y2=2px(p>0)相交于点A,与抛物线的准线相交于点B,点N为AB的中点.(1)求抛物线的方程;
(2)过点M(m,0)(m<0)作斜率为$\frac{{\sqrt{3}}}{3}$的直线与抛物线y2=2px相交于C,D两点,F为抛物线的焦点,如果
|CD|2=$\frac{64}{13}$|FC|•|FD|,求∠CFD的余弦值.
分析 (1)求出N(1,0),可设$B(-\frac{p}{2},{y_0})$,求出A点的坐标,代入抛物线方程,解得p=2,即可求出抛物线的方程.
(2)联立直线与抛物线方程,利用判别式求出m的范围,设C(x1,y1),D(x2,y2),利用韦达定理,弦长公式,求解|CD|2=$\frac{64}{13}$|FC|•|FD|,两侧数据,利用向量的数量积化简,求解即可.
解答 解:(1)由题意得N(1,0),可设$B(-\frac{p}{2},{y_0})$,
由点N为AB的中点得A点的坐标为$A(2+\frac{p}{2},-{y_0})$,
所以${(-{y_0})^2}=2p(2+\frac{p}{2})$且${y_0}=\sqrt{3}(-\frac{p}{2}-1)$,解得p=2或p=-6(舍去),
所以抛物线的方程为y2=4x.
(2)把$y=\frac{{\sqrt{3}}}{3}(x-m)$代入y2=4x得x2-(2m+12)x+m2=0,
因为△=4m2+48m+144-4m2>0,所以m>-3,
设C(x1,y1),D(x2,y2),
则${x_1}+{x_2}=2m+12,{x_1}{x_2}={m^2}$,
$|{CD}|=\sqrt{1+{{(\frac{{\sqrt{3}}}{3})}^2}}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\frac{2}{3}\sqrt{3}•\sqrt{48m+144}$,$|{FC}|•|{FD}|=({x_1}+1)•({x_2}+1)={x_1}{x_2}+{x_1}+{x_2}+1={m^2}+2m+13$,
由13|CD|2=64|FC|•|FD|得$\frac{4}{3}(48m+144)•13=64•({m^2}+2m+13)$,
解得m=-2或m=13(舍去),
因为${y_1}•{y_2}=\frac{1}{3}({x_1}-m)({x_2}-m)=\frac{1}{3}[{x_1}{x_2}-m({x_1}+{x_2})+{m^2}]=-4m$
又$\overrightarrow{FC}•\overrightarrow{FD}=({x_1}-1,{y_1})•({x_2}-1,{y_2})={x_1}{x_2}-({x_1}+{x_2})+1+{y_1}{y_2}={m^2}-6m-11=5$,
因为$|{FC}|•|{FD}|=({x_1}+1)•({x_2}+1)={x_1}{x_2}+{x_1}+{x_2}+1={m^2}+2m+13=13$,
所以由$\overrightarrow{FC}•\overrightarrow{FD}=|{FC}|•|{FD}|•cos∠CFD$,
得$cos∠CFD=\frac{5}{13}$.
点评 本题考查抛物线方程的求法,直线与抛物线的位置关系,向量在平面解析几何中的应用,考查转化思想以及计算能力.

| A. | $\overrightarrow{e_1}$,2$\overrightarrow{e_2}$ | B. | $\overrightarrow{e_1}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | ||
| C. | -$\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | D. | $\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ |
 如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠BAD=60°,PA⊥PC,
如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠BAD=60°,PA⊥PC,PB=PD,二面角P-BD-A为60°,则|PC|=( )
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 2 |
 某三棱锥的三视图如图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$.
某三棱锥的三视图如图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$. 根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.
根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.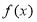 是定义在
是定义在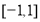 上的奇函数且
上的奇函数且 ,当
,当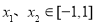 ,且
,且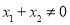 时,有
时,有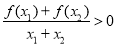 ,若
,若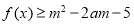 对所有
对所有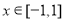 、
、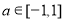 恒成立,则实数
恒成立,则实数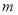 的取值范围是________.
的取值范围是________.