题目内容
11. 如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠BAD=60°,PA⊥PC,
如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠BAD=60°,PA⊥PC,PB=PD,二面角P-BD-A为60°,则|PC|=( )
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 2 |
分析 连接AC,AC∩BD=O,则BD⊥AC,求出∠POA=60°,利用PA⊥PC,可得∠PAC=60°,PC=ACsin60°,求出AC,即可得出结论.
解答  解:连接AC,AC∩BD=O,则BD⊥AC,
解:连接AC,AC∩BD=O,则BD⊥AC,
∵PB=PD,∴BD⊥PO,
∵二面角P-BD-A为60°,
∴∠POA=60°,
∵PA⊥PC,
∴∠PAC=60°,
∴PC=ACsin60°,
∵ABCD是边长为2的菱形,且∠BAD=60°,
∴AC=2$\sqrt{3}$,
∴PC=3,
故选C.
点评 本题考查二面角,考查空间距离的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
19.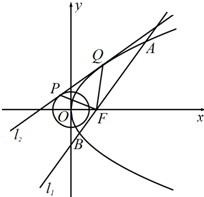 如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )
如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )
 如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )
如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{{\sqrt{3}}}{4}$ | D. | 1 |
 ,且
,且 ,
, ,则
,则 的取值范围是_______.
的取值范围是_______.