题目内容
13. 某三棱锥的三视图如图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$.
某三棱锥的三视图如图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$.
分析 根据几何体的三视图得出该三棱锥的侧面垂直于底面,求出四个面的面积即可得出结论.
解答 解:根据三视图得,该三棱锥的直观图如图所示,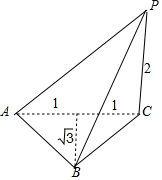
该三棱锥中,侧面PAC⊥底面ABC,
S△ABC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
S△PAC=$\frac{1}{2}$×2×2=2,
S△PBC=$\frac{1}{2}$×2×$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2,
S△PAB=$\frac{1}{2}$×2×$\sqrt{{2}^{2}{+2}^{2}{-(\frac{2}{2})}^{2}}$=$\sqrt{7}$;
三棱锥的四个面中,面积最大的面PAB的面积是$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题主要考查了三视图的识别和应用问题,根据三视图确定三棱锥的各面面积是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 标记.
标记.
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时有
时有 .
.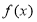 的解析式;
的解析式; 的值域;
的值域;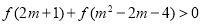 ,求
,求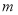 的取值范围.
的取值范围.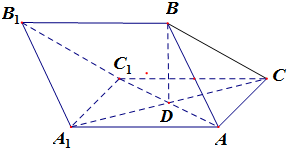 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.