题目内容
19. 如图,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=1,AB∥DC,AD⊥CD,PC⊥平面ABCD.
如图,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=1,AB∥DC,AD⊥CD,PC⊥平面ABCD.(Ⅰ)求证:BC⊥平面PAC;
(Ⅱ)若M为线段PA的中点,且过C,D,M三点的平面与线段PB交于点N,确定点N的位置,并说明理由.
分析 (I)连接AC,推导出AC⊥BC,PC⊥BC,由此能证明BC⊥平面PAC.
(II)当N为PB的中点时,由M为PA的中点,得到MN∥AB,且MN=$\frac{1}{2}AB=2a$.再由AB∥CD,得MN∥CD从而求出点N为过C,D,M三点的平面与线段PB的交点.
解答 解:(I)连接AC,在直角梯形ABCD中,AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{2}$,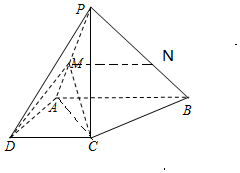
BC=$\sqrt{(AB-CD)^{2}+A{D}^{2}}$=$\sqrt{2}$,
∴AC2+BC2=AB2,即AC⊥BC.
又PC⊥平面ABCD,∴PC⊥BC,
又AC∩PC=C,故BC⊥平面PAC.
解:(II)N为PB的中点.
理由如下:
∵N为PB的中点,M为PA的中点,
∴MN∥AB,且MN=$\frac{1}{2}AB=2a$.
又∵AB∥CD,∴MN∥CD,∴M,N,C,D四点共面,
∴点N为过C,D,M三点的平面与线段PB的交点.
点评 本题考查线面垂直的证明,考查点的位置的确定,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
10.下列各式正确的是( )
| A. | tan(-$\frac{13}{4}$π)<tan(-$\frac{17}{5}$π) | B. | tan(-$\frac{13}{4}$π)>tan(-$\frac{17}{5}$π) | ||
| C. | tan(-$\frac{13}{4}$π)=tan(-$\frac{17}{5}$π) | D. | 大小关系不确定 |
11.设集合M={x|x2-2x-3≥0},N={x|-3<x<3},则( )
| A. | M⊆N | B. | N⊆M | C. | M∪N=R | D. | M∩N=∅ |
8.已知直线l1:(k+1)x+y+1=0和l2:(k-3)x-ky-1=0,若l1与l2有公共点,则k的取值范围为( )
| A. | k≠1且k≠-3 | B. | k≠-3 | C. | k=1 | D. | k=1且k=-3 |
9.在正方体ABCD-A1B1C1D1中,直线BB1与平面ACD1所成角的余弦值为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
 为实数,
为实数,
 记集合
记集合
 若
若 分别为集合S,T的元素个数,则下列结论
分别为集合S,T的元素个数,则下列结论 的是( )
的是( )


