题目内容
已知F是双曲线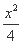 -
-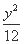 =1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为 .
=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为 .
9
解析:由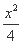 -
-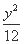 =1知c2=4+12=16,
=1知c2=4+12=16,
c=4.
∴左焦点F(-4,0),设双曲线右焦点为F′(4,0),
∵点P在双曲线右支上,
∴|PF|-|PF′|=2a=4,
∴|PF|=4+|PF′|,
∴|PF|+|PA|=4+|PF′|+|PA|.
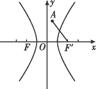
由图可知,当A、P、F′三点共线时,|PF′|+|PA|最小,此时,
(|PF|+|PA|)min =4+(|PF′|+|PA|)min
=4+|AF′|
=4+
=4+5
=9.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
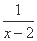 (x>2)在x=a处取最小值,则a等于( )
(x>2)在x=a处取最小值,则a等于( )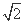 (B)1+
(B)1+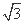 (C)3 (D)4
(C)3 (D)4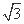 ,sin x),x∈R.
,sin x),x∈R.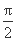 ),证明:a和b不平行;
),证明:a和b不平行; (B)
(B) (C)
(C) (D)
(D)
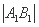 =
=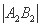 ,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )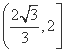 (B)
(B) 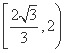
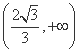 (D)
(D) 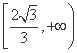
 x与双曲线
x与双曲线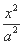 -
-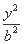 =1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e= .
=1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e= . 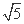 ,则该双曲线的标准方程为 .
,则该双曲线的标准方程为 .  +
+ =1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-
=1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x- )2+y2=
)2+y2= 相切于点Q,且
相切于点Q,且 =2
=2 ,则椭圆C的离心率等于( )
,则椭圆C的离心率等于( ) (B)
(B) (C)
(C) (D)
(D)