题目内容
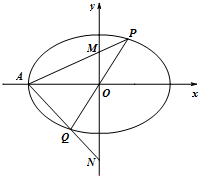 如图,在平面直角坐标系xOy中,离心率为
如图,在平面直角坐标系xOy中,离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(1)求椭圆C的标准方程;
(2)试问以MN为直径的圆是否经过定点(与直线PQ的斜率无关)?请证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:,(1)设P(x0,
x0),由于直线PQ斜率为
时,PQ=2
,可得x02+(
x0)2=3,解得x02=2,代入椭圆方程可得:
+
=1,又e=
=
=
,联立解得即可.
(2)设P(x0,y0),则Q(-x0,-y0),代入椭圆方程可得
+2
=4.由直线PA方程为:y=
(x+2),可得M(0,
),同理由直线QA方程可得N(0,
),可得以MN为直径的圆为(x-0)(x-0)+(y-
)(y-
)=0,由于
-4=-2
,代入整理即可得出.
| ||
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| a2 |
| 1 |
| b2 |
| c |
| a |
| ||
| a |
| ||
| 2 |
(2)设P(x0,y0),则Q(-x0,-y0),代入椭圆方程可得
| x | 2 0 |
| y | 2 0 |
| y0 |
| x0+2 |
| 2y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| 2y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| x | 2 0 |
| y | 2 0 |
解答:
解:(1)设P(x0,
x0),
∵直线PQ斜率为
时,PQ=2
,
∴x02+(
x0)2=3,
∴x02=2,(
x0)2=1,
∴
+
=1,
∵e=
=
=
,化为a2=2b2.
联立
,
∴a2=4,b2=2.
∴椭圆C的标准方程为
+
=1.
(2)以MN为直径的圆过定点F(±
,0).下面给出证明:
设P(x0,y0),则Q(-x0,-y0),且
+
=1,即
+2
=4,
∵A(-2,0),∴直线PA方程为:y=
(x+2),
∴M(0,
),
直线QA方程为:y=
(x+2),
∴N(0,
),
以MN为直径的圆为(x-0)(x-0)+(y-
)(y-
)=0,
即x2+y2-
y+
=0,
∵
-4=-2
,
∴x2+y2+
y-2=0,
令y=0,x2+y2-2=0,解得x=±
,
∴以MN为直径的圆过定点F(±
,0).
| ||
| 2 |
∵直线PQ斜率为
| ||
| 2 |
| 3 |
∴x02+(
| ||
| 2 |
∴x02=2,(
| ||
| 2 |
∴
| 2 |
| a2 |
| 1 |
| b2 |
∵e=
| c |
| a |
| ||
| a |
| ||
| 2 |
联立
|
∴a2=4,b2=2.
∴椭圆C的标准方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)以MN为直径的圆过定点F(±
| 2 |
设P(x0,y0),则Q(-x0,-y0),且
| ||
| 4 |
| ||
| 2 |
| x | 2 0 |
| y | 2 0 |
∵A(-2,0),∴直线PA方程为:y=
| y0 |
| x0+2 |
∴M(0,
| 2y0 |
| x0+2 |
直线QA方程为:y=
| y0 |
| x0-2 |
∴N(0,
| 2y0 |
| x0-2 |
以MN为直径的圆为(x-0)(x-0)+(y-
| 2y0 |
| x0+2 |
| 2y0 |
| x0-2 |
即x2+y2-
| 4x0y0 |
| x02-4 |
| 4y02 |
| x02-4 |
∵
| x | 2 0 |
| y | 2 0 |
∴x2+y2+
| 2x0 |
| y0 |
令y=0,x2+y2-2=0,解得x=±
| 2 |
∴以MN为直径的圆过定点F(±
| 2 |
点评:本题考查了椭圆与圆的标准方程及其性质、直线与椭圆相交问题、点与椭圆的位置关系、点斜式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
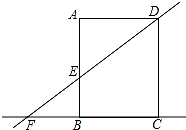 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.