题目内容
已知函数f(x)=
是奇函数,M={y|y=f(x),x<0},N={x|ax-a+2>0},M⊆N
(1)若实数m的值及a的取值范围;
(2)若函数f(x)在区间[-1,t-2]上单调递增,求实数t的取值范围.
|
(1)若实数m的值及a的取值范围;
(2)若函数f(x)在区间[-1,t-2]上单调递增,求实数t的取值范围.
考点:函数单调性的性质,函数奇偶性的性质,分段函数的应用
专题:函数的性质及应用
分析:(1)由题意可得f(x)+f(-x)=0,求得m=2,f(x)=
,求得f(x)的值域,可得M,由M⊆N,N={x|ax>a-2},求得a的范围.
(2)若函数f(x)在区间[-1,t-2]上单调递增,结合函数f(x)的图象可得-1<t-2≤1,求得实数t的取值范围.
|
(2)若函数f(x)在区间[-1,t-2]上单调递增,结合函数f(x)的图象可得-1<t-2≤1,求得实数t的取值范围.
解答:
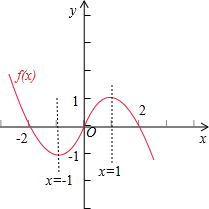 解:(1)设x<0,则-x>0,由函数f(x)=
解:(1)设x<0,则-x>0,由函数f(x)=
是奇函数,
可得f(x)+f(-x)=0,即x2+mx+(-x2-2x)=0,求得m=2,
f(x)=
.
M={y|y=f(x),x<0}={y|y≥(-1)2+2(-1)=-1}={y|y≥-1},
由M⊆N,N={x|ax>a-2},可得 a≥0,且
<-1,求得0≤a<1.
(2)若函数f(x)在区间[-1,t-2]上单调递增,
结合函数f(x)的图象可得-1<t-2≤1,求得1<t≤3,
故要求的实数t的取值范围为(1,3].
 解:(1)设x<0,则-x>0,由函数f(x)=
解:(1)设x<0,则-x>0,由函数f(x)=
|
可得f(x)+f(-x)=0,即x2+mx+(-x2-2x)=0,求得m=2,
f(x)=
|
M={y|y=f(x),x<0}={y|y≥(-1)2+2(-1)=-1}={y|y≥-1},
由M⊆N,N={x|ax>a-2},可得 a≥0,且
| a-2 |
| a |
(2)若函数f(x)在区间[-1,t-2]上单调递增,
结合函数f(x)的图象可得-1<t-2≤1,求得1<t≤3,
故要求的实数t的取值范围为(1,3].
点评:本题主要求函数的奇偶性、单调性,二次函数的性质,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
下列函数中,在其定义域上既是奇函数又是增函数的是( )
| A、y=x2 | ||
| B、y=x-1 | ||
C、y=x
| ||
| D、y=x3 |
已知抛物线y2=2px与直线ax+y-4=0的一个交点是(1,2),则抛物线的焦点到该直线的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
利用直接插入顺序法将数据6插入序列{1,3,5,7,9,11,13}中需要作大小比较的次数为( )
| A、3 | B、4 | C、5 | D、6 |

 如图,在平面直角坐标系xOy中,离心率为
如图,在平面直角坐标系xOy中,离心率为