题目内容
设向量
=(1,2,3),
=(-1,y,z),且
∥
,则y= ,z= .
| a |
| b |
| a |
| b |
考点:向量的数量积判断向量的共线与垂直
专题:平面向量及应用
分析:利用向量共线定理即可得出.
解答:
解:∵
∥
,
∴存在实数k使得
=k
,
∴
,解得y=-2,z=-3.
故答案分别为:-2;-3.
| a |
| b |
∴存在实数k使得
| a |
| b |
∴
|
故答案分别为:-2;-3.
点评:本题考查了向量共线定理,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
已知抛物线y2=2px与直线ax+y-4=0的一个交点是(1,2),则抛物线的焦点到该直线的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在(
+
)12的展开式中,x项的系数为( )
| x |
| 1 | |||
|
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
利用直接插入顺序法将数据6插入序列{1,3,5,7,9,11,13}中需要作大小比较的次数为( )
| A、3 | B、4 | C、5 | D、6 |
等差数列{an}的前n项和为Sn,若S15为一确定常数,下列各式也为确定常数的是( )
| A、a2+a13 |
| B、a2+a7+a12 |
| C、a3+a6+a15 |
| D、a1a8a15 |
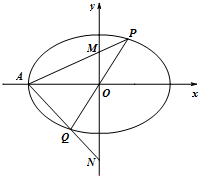 如图,在平面直角坐标系xOy中,离心率为
如图,在平面直角坐标系xOy中,离心率为