题目内容
已知数列{an}是公比为正整数的等比数列,若a2=2且a1,a3+
,a4成等差数列,定义:
为n个正数P1,P2,…,Pn(n∈N*)的“均倒数”
(1)若数列{bn}前n项的“均倒数“为
(n∈N*),求数列{bn}的通项bn
(2)试比较
+
+…+
与2的大小,并说明理由.
| 1 |
| 2 |
| n |
| P1+P2+…+Pn |
(1)若数列{bn}前n项的“均倒数“为
| 1 |
| 2an-1 |
(2)试比较
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
考点:数列的求和,等比数列的性质,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知得
,由q为正整数,解得a1=1,q=2,从而an=2n-1,设数列{bn}前n项的前n项和为Sn,进而得到Sn=n•2n-n,由此能求出bn=(n+1)•2n-1-1.
(2)由
=
<
=
<
,利用放缩法和等比数列的性质能求出
+
+…+
<2.
|
(2)由
| 1 |
| bn |
| 1 |
| n•2n-1+2n-1-1 |
| 1 |
| n•2n-1 |
| 2 |
| n•2n |
| 2 |
| 2n |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
解答:
解:(1)∵数列{an}是公比为正整数的等比数列,
a2=2且a1,a3+
,a4成等差数列,
∴
,
由q为正整数,解得a1=1,q=2,
∴an=2n-1,
∵数列{bn}前n项的“均倒数“为
(n∈N*),
∴
(b1+b2+…+bn)=2an-1=2n-1,
设数列{bn}前n项的前n项和为Sn,则Sn=n•2n-n,
∴b1=1×2-1=1,
n≥2时,bn=Sn-Sn-1=(n•2n-n)-[(n-1)•2n-1-(n-1)]=(n+1)•2n-1-1,
n=1时,上式成立,
∴bn=(n+1)•2n-1-1.
(2)解:∵
=
<
=
<
,
∴
+
+…+
<2(
+
+…+
)
=2×
=2(1-
)<2.
∴
+
+…+
<2.
a2=2且a1,a3+
| 1 |
| 2 |
∴
|
由q为正整数,解得a1=1,q=2,
∴an=2n-1,
∵数列{bn}前n项的“均倒数“为
| 1 |
| 2an-1 |
∴
| 1 |
| n |
设数列{bn}前n项的前n项和为Sn,则Sn=n•2n-n,
∴b1=1×2-1=1,
n≥2时,bn=Sn-Sn-1=(n•2n-n)-[(n-1)•2n-1-(n-1)]=(n+1)•2n-1-1,
n=1时,上式成立,
∴bn=(n+1)•2n-1-1.
(2)解:∵
| 1 |
| bn |
| 1 |
| n•2n-1+2n-1-1 |
| 1 |
| n•2n-1 |
| 2 |
| n•2n |
| 2 |
| 2n |
∴
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
=2×
| ||||
1-
|
=2(1-
| 1 |
| 2n |
∴
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
点评:本题考查数列的通项公式的求法,考查数列的前n项和与2的大小的比较,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知复数z=
(其中i是虚数单位),则复数z在坐标平面内对应的点在( )
| 1+i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某空间几何体的三视图如图所示,则这个空间几何体的表面积是( )


| A、2π+4 | B、3π+4 |
| C、4π+4 | D、4π+6 |
双曲线
-
=-1与抛物线y=
x2有一个公共焦点F,双曲线上过点F且垂直实轴的弦长为
,则双曲线的离心率等于( )
| x2 |
| b2 |
| y2 |
| a2 |
| 1 |
| 8 |
2
| ||
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
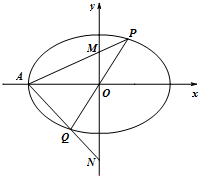 如图,在平面直角坐标系xOy中,离心率为
如图,在平面直角坐标系xOy中,离心率为