题目内容
6.已知17x=100,1.7y=100,求$\frac{1}{x}-\frac{1}{y}$的值.分析 利用指对互化公式得出x,y,利用对数的运算性质得出$\frac{1}{x}$,$\frac{1}{y}$.
解答 解:∵17x=100,1.7y=100,
∴x=log17100,y=log1.7100.
∴$\frac{1}{x}$=log10017,$\frac{1}{y}$=log1001.7.
∴$\frac{1}{x}-\frac{1}{y}$=log10010=$\frac{1}{2}$.
点评 本题考查了对数的运算性质,属于基础题.

练习册系列答案
相关题目
18.若动点A(x1,y1),B(x2,y2)分别在直线l1:x+y-2=0和l2:x+y-6=0上移动,则AB中点M到原点距离的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
13.经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段没有公共点,则直线l的斜率k与倾斜角α的取值范围分别是( )
| A. | (-∞,-1)∪(1,+∞),($\frac{π}{4}$,$\frac{3π}{4}$) | B. | (-∞,-1)∪(1,+∞),($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$) | ||
| C. | (-1,1),[$\frac{π}{4}$,$\frac{3π}{4}$] | D. | (-1,1),[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,0) |
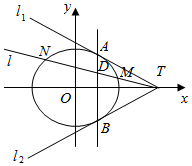 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.