题目内容
5．四边形ABCD中，设$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，那么$\overrightarrow{AC}$+$\overrightarrow{BD}$=（ ）| A． | $\overrightarrow{a}-\overrightarrow{b}$ | B． | $\overrightarrow{a}+\overrightarrow{b}$ | C． | $\overrightarrow{b}-\overrightarrow{a}$ | D． | 不能确定 |
分析 根据向量加法的三角形法则可知$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AB}+\overrightarrow{b}$，$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}$=$\overrightarrow{BA}+\overrightarrow{a}$．
解答 解：$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AB}+\overrightarrow{b}$，$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{a}$．
∴$\overrightarrow{AC}+\overrightarrow{BD}$=$\overrightarrow{AB}+\overrightarrow{b}$+（-$\overrightarrow{AB}+\overrightarrow{a}$）=$\overrightarrow{a}+\overrightarrow{b}$．
故选：B．
点评 本题考查了平面向量加法的三角形法则，属于基础题．
练习册系列答案
相关题目
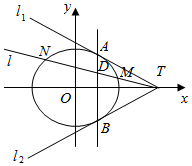已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1（a＞0）的两条切线方程y=±$\frac{1}{2}$（x-4），切点分别为A、B，且切线与x轴的交点为T．
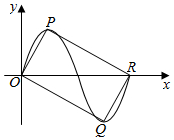如图，四边形OQRP为矩形，其中P，Q分别是函数f（x）=$\sqrt{3}$sinwx（A＞0，w＞0）图象上的一个最高点和最低点，O为坐标原点，R为图象与x轴的交点．