题目内容
10.将点P的直角坐标(-$\sqrt{3}$,-1)化成极坐标( )| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{π}{2}$) | C. | (2,$\frac{4π}{3}$) | D. | (2,$\frac{7π}{6}$) |
分析 由点的直角坐标求出点P的极径,然后求出极角得答案.
解答 解:由点P(-$\sqrt{3}$,-1),得ρ=|OP|=$\sqrt{(-\sqrt{3})^{2}+(-1)^{2}}=2$,
如图,
由x=ρcosθ,得cosθ=$\frac{x}{ρ}=\frac{-\sqrt{3}}{2}$,∴θ=$\frac{7π}{6}$.
则P的极坐标为(2,$\frac{7π}{6}$).
故选:D.
点评 本题考查点的直角坐标化极坐标,是基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.已知函数f(x)=$\sqrt{3}$sin(2x+$\frac{π}{3}$),其中x∈R,下列结论中正确的是( )
| A. | f(x)是最小正周期为π的偶函数 | |
| B. | f(x)的一条对称轴是 $x=\frac{π}{3}$ | |
| C. | f(x)的最大值为2 | |
| D. | 将函数$y=\sqrt{3}sin2x$的图象向左平移$\frac{π}{6}$个单位得到函数f(x)的图象 |
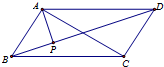 如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.