已知双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1在左支上一点M到右焦点F1的距离为16.N是线段MF1的中点.O为坐标原点.则|ON|等( )A．4B．3C．2D．1 题目和参考答案——青夏教育精英家教网—

题目内容

11．已知双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1在左支上一点M到右焦点F₁的距离为16，N是线段MF₁的中点，O为坐标原点，则|ON|等（　　）

A．

B．

C．

D．

分析由题意，根据中位线定理及双曲线的定义即可求得丨MF₂丨=6，则丨ON丨=3．

解答解：设椭圆的左焦点F₂，由题意可知：丨ON丨∥$\frac{1}{2}$丨MF₂丨，则丨MF₁丨-丨MF₂丨=2a=10，
丨MF₂丨=6，则丨ON丨=3，
故选B．

点评本题考查双曲线的定义，中位线定理，考查计算能力，属于基础题．

练习册系列答案

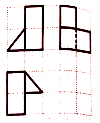
$\frac{2\sqrt{2}}{3}$

D．

1+$\frac{2\sqrt{2}}{3}$

2．已知a，b，c∈R，则下列推证中正确的是（　　）

	A．	a＞b⇒am²＞bm²		B．	$\frac{a}{c}＞\frac{b}{c}$⇒a＞b
	C．	ac²＞bc²⇒a＞b		D．	a²＞b²，ab＞0⇒$\frac{1}{a}＜\frac{1}{b}$

19．在直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数），直线l的方程为x+$\sqrt{3}$y-9=0，以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C和直线l的极坐标方程；
（2）射线OA：θ=$\frac{π}{6}$与圆C的交点是O，M，与直线l的交点为N，求线段MN的长．

6．用0，1，2，3，4这五个数字可以组成36 个没有重复数字的四位奇数．

2．已知等差数列{a_n}中，a₂，a₂₀₁₆是方程x²-2x-2=0的两根，则S₂₀₁₇=（　　）

9．

某三棱锥的三视图如图所示，其中俯视图是一个等腰直角三角形，则该三棱锥的外接球的表面积为（　　）

$\frac{{5\sqrt{5}π}}{6}$

6．为了解高中生上学使用手机情况，调查者进行了如下的随机调查：调查者向被调查者提出两个问题：（1）你的学号是奇数吗？（2）你上学时是否经常带手机？要求被调查者背对着调查人员抛掷一枚硬币，如果出现正面，就回答第一问题，否则就回答第二个问题．被调查者不必告诉调查人员自己回答的是哪一个问题，只需回答“是”或“不是”，因为只有被调查者本人知道回答了哪一个问题，所以都如实地做了回答．结果被调查的800人（学号从1至800）中有260人回答了“是”．由此可以估计这800人中经常带手机上学的人数是120．

7．已知F₁、F₂分别是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，A为椭圆的上顶点，O为坐标原点，N（-2，0），并且满足$\overrightarrow{F{{\;}_{1}F}_{2}}$=2$\overrightarrow{N{F}_{1}}$，$\overrightarrow{AN}$•$\overrightarrow{A{F}_{1}}$=3
（Ⅰ）求此椭圆的方程；
（II）若过点N的直线l与椭圆交于不同的两点E、F（E在N、F之间），$\overrightarrow{NE}$=λ$\overrightarrow{NF}$，试求实数λ的取值范围．

试题分类