题目内容
实数m为何值时，复数z=（m2+5m+6）+（m2-2m-15）i 对应的点在：
（1）x轴上方；
（2）直线x+y+5=0上．
（1）x轴上方；
（2）直线x+y+5=0上．
考点：复数的代数表示法及其几何意义
专题：计算题,数系的扩充和复数
分析：（1）由题意得，m2-2m-15＞0，解出即可；
（2）由题意得，（m2+5m+6）+（m2-2m-15）+5=0，解出可得答案；
（2）由题意得，（m2+5m+6）+（m2-2m-15）+5=0，解出可得答案；
解答：
解：（1）若复数Z对应的点在x轴上方，
则m2-2m-15＞0，解得m＜-3或m＞5．
（2）复数z对应的点为（m2+5m+6，m2-2m-15），
∵z对应的点在直线x+y+5=0上，
∴（m2+5m+6）+（m2-2m-15）+5=0，整理得2m2+3m-4=0，
解得m=
．
则m2-2m-15＞0，解得m＜-3或m＞5．
（2）复数z对应的点为（m2+5m+6，m2-2m-15），
∵z对应的点在直线x+y+5=0上，
∴（m2+5m+6）+（m2-2m-15）+5=0，整理得2m2+3m-4=0，
解得m=
-3±
| ||
| 4 |
点评：该题考查复数的代数表示法及其几何意义，属基础题，熟记复数的几何意义是解题关键．
练习册系列答案
相关题目
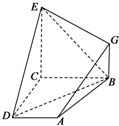如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=
如图，已知四棱锥P-ABCD的底面是矩形，侧面PAB是正三角形，且平面PAB⊥平面ABCD，E是PA的中点，AC与BD的交点为M．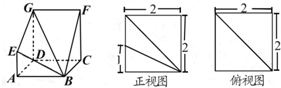
如图，多面体ABCD-EFG中，底面ABCD为正方形，GD∥FC∥AE，AE⊥平面ABCD，其正视图、俯视图及相关数据如图：