题目内容
已知函数f(x)=
sinωx-2sin2
+m(ω>0)的最小正周期为3π,且当x∈[0,π]时,函数f(x)的最小值为0.
(1)求函数f(x)的表达式;
(2)在△ABC中,角角A、B、C所对的边分别为a、b、c,若f(c)=1且a+b=10,求△ABC面积的最大值.
| 3 |
| ωx |
| 2 |
(1)求函数f(x)的表达式;
(2)在△ABC中,角角A、B、C所对的边分别为a、b、c,若f(c)=1且a+b=10,求△ABC面积的最大值.
考点:正弦定理的应用,三角函数中的恒等变换应用,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:解三角形
分析:(1)利用两角和公式和二倍角公式对函数解析式化简,根据函数的周期求得ω,根据函数的最小值求得m,则函数的解析式可得.
(2)先根据f(c)=1,求得C,进而根据三角形面积公式和基本不等式求得三角形面积的最大值.
(2)先根据f(c)=1,求得C,进而根据三角形面积公式和基本不等式求得三角形面积的最大值.
解答:
解:(1)f(x)=
sinωx-2sin2
+m=
sinωx-cosωx+m-1=2sin(ωx-
)+m-1,
∵函数的最小正周期为3π,
∴
=3π,ω=
∴f(x)=2sin(
x-
)+m-1,
∵x∈[0,π],
∴
x-
∈[-
,
],
∴f(x)min=-
×2+m-1=0,
∴m=2,
∴f(x)=2sin(
x-
)+m-1.
(2)f(c)=2sin(
C-
)+1=1,
∴sin(
C-
)=0,
∴
C-
=0,C=
,
∴S△ABC=
absinC=
ab≤
•
=
×
=
,
即三角形面积最大值为
.
| 3 |
| ωx |
| 2 |
| 3 |
| π |
| 6 |
∵函数的最小正周期为3π,
∴
| 2π |
| ω |
| 2 |
| 3 |
∴f(x)=2sin(
| 2 |
| 3 |
| π |
| 6 |
∵x∈[0,π],
∴
| 2 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴f(x)min=-
| 1 |
| 2 |
∴m=2,
∴f(x)=2sin(
| 2 |
| 3 |
| π |
| 6 |
(2)f(c)=2sin(
| 2 |
| 3 |
| π |
| 6 |
∴sin(
| 2 |
| 3 |
| π |
| 6 |
∴
| 2 |
| 3 |
| π |
| 6 |
| π |
| 4 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| (a+b)2 |
| 4 |
| ||
| 4 |
| 100 |
| 4 |
25
| ||
| 4 |
即三角形面积最大值为
25
| ||
| 4 |
点评:本题主要考查了三角函数恒等变换的应用,基本不等式的应用.考查了学生对基础知识的综合运用.

练习册系列答案
相关题目
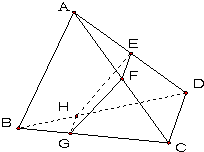 如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,
如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,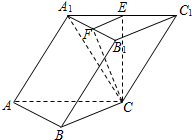 在斜三棱柱ABC-A1B1C1中,已知侧面ACC1A1⊥底面ABC,A1C=C1C,E,F分别是A1C1、A1B1的中点.
在斜三棱柱ABC-A1B1C1中,已知侧面ACC1A1⊥底面ABC,A1C=C1C,E,F分别是A1C1、A1B1的中点.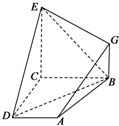 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= 如图,已知四棱锥P-ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M.
如图,已知四棱锥P-ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M.