题目内容

已知函数A={x||2x-1|＜1}，B={x|x2-2ax+a2-1＞0}，若A⊆B，求实数a的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：通过解绝对值不等式，一元二次不等式分别求出集合A=（0，1），B=（-∞，a-1）∪（a+1，+∞），而由A⊆B便可得到1≤a-1，或0≥a+1，这样解出a即得a的取值范围．
解答： 解：A=（0，1），B=（-∞，a-1）∪（a+1，+∞），A⊆B；
∴1≤a-1，或0≥a+1；
∴a≥2，或a≤-1；
∴实数a的取值范围为[2，+∞）∪（-∞，-1]．
点评：考查绝对值不等式、一元二次不等式的解法，以及子集的概念．
练习册系列答案
相关题目
27 
2
3
+16 -
1
2
-（
1
2
）-2-（
8
27
） -
2
3
=
 
．
由曲线y=x2和直线y=0，x=1，y=
1
4
所围成的封闭图形的面积为（　　）
A、
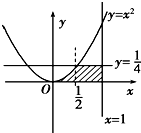
1
6
B、
1
3
C、
1
2
D、
2
3
设函数f（x）=
cos2θ
6
x3+
3
sin2θ
2
x2-tan2θ，其中θ∈（0，
2π
3
]，若g（x）=f′（x），则g′（-1）的取值范围是（　　）
A、[-2，2]
B、[-
2
，
3
]
C、[-1，2]
D、[-
2
，2]
函数f（x）=3sin（2x+
π
6
）的部分图象如图所示．
（1）写出f（x）的最小正周期及图中x0、y0的值；
（2）求f（x）在区间[
π
12
，
π
2
]上的最大值和最小值．
在△ABC中，有
a
sinA
=
b
cosB
，则B的大小为
 
．
已知函数f（x）=2sinx（sinx+cosx），x∈R．
（1）求f（x）的最小正周期T和最大值M；
（2）若f(
α
2
+
π
8
)=-
1
3
，求cosα的值．
已知数列{an}的前n项和为Sn，若an=sin
nπ
3
，则S2014=
 
．
若复数z满足（1+i）z=1-i，则
.
z
=（　　）
A、1B、-1C、iD、-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网