题目内容
8.已知tanα=2,则tan2α的值为-$\frac{3}{4}$,cos2α=-$\frac{3}{5}$.分析 由条件利用二倍角的正切公式、二倍角的余弦公式,求得要求式子的值.
解答 解:∵tanα=2,则tan2α=$\frac{2tanα}{1{-tan}^{2}α}$=$\frac{4}{1-4}$=-$\frac{4}{3}$,
cos2α=$\frac{{cos}^{2}α{-sin}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{1{-tan}^{2}α}{{tan}^{2}α+1}$=-$\frac{3}{5}$,
故答案为:-$\frac{4}{3}$;-$\frac{3}{5}$.
点评 本题主要考查二倍角的正切公式、二倍角的余弦公式的应用,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.已知函数y=lgx的定义域为集合A,集合B={0,1,2},则A∩B=( )
| A. | (0,+∞) | B. | (0,2] | C. | {0,1,2} | D. | {1,2} |
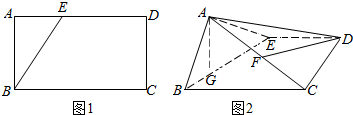
 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
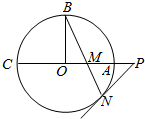
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P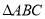 中,
中,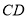 是
是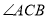 的角平分线,
的角平分线,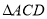 的外接圆交
的外接圆交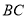 于
于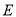 点.
点.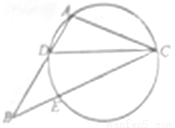
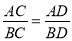 ;
;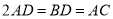 ,求
,求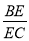 的值.
的值.