题目内容
19．已知函数f（x）=$\left\{\begin{array}{l}{lgx，x≥\frac{3}{2}}\\{lg（3-x），x＜\frac{3}{2}}\end{array}\right.$，若方程f（x）=k有实数解，则实数k的取值范围是[lg$\frac{3}{2}$，+∞）．分析 作函数f（x）=$\left\{\begin{array}{l}{lgx，x≥\frac{3}{2}}\\{lg（3-x），x＜\frac{3}{2}}\end{array}\right.$的图象，从而可得f（x）≥lg$\frac{3}{2}$，从而解得．
解答 解：作函数f（x）=$\left\{\begin{array}{l}{lgx，x≥\frac{3}{2}}\\{lg（3-x），x＜\frac{3}{2}}\end{array}\right.$的图象如下，
结合图象可知，f（x）≥lg$\frac{3}{2}$，
故实数k的取值范围是[lg$\frac{3}{2}$，+∞）；
故答案为：[lg$\frac{3}{2}$，+∞）．
点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用．
练习册系列答案
相关题目
12．（1）在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩：
甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；
乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；
用茎叶图表示甲，乙两个成绩；并根据茎叶图分析甲、乙两人成绩；
（2）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
（I）求回归直线方程$\stackrel{∧}{y}$=bx+a，其中b=-20，a=$\stackrel{∧}{y}$-b$\overline{x}$
（Ⅱ）预计在今后的销售中，销量与单价仍然服从（I）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）
甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；
乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；
用茎叶图表示甲，乙两个成绩；并根据茎叶图分析甲、乙两人成绩；
（2）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
（Ⅱ）预计在今后的销售中，销量与单价仍然服从（I）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）
4．已知f（x）是偶函数，且在[0，1]上是增函数，则f（0.5）、f（-1）、f（0）的大小关系是（ ）
| A． | f（0.5）＜f（0）＜f（-1） | B． | f（-1）＜f（0.5）＜f（0） | C． | f（0）＜f（0.5）＜f（-1） | D． | f（-1）＜f（0）＜f（0.5） |
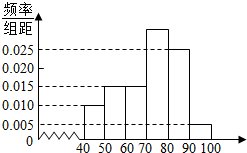某校高一（2）班共有60名同学参加期末考试，现将其数学学科成绩（均为整数）分成六个分数段[40，50），[50，60），…，[90，100]，画出如如图所示的部分频率分布直方图，请观察图形信息，回答下列问题：