题目内容
已知正项数列{an}的前n项和为Sn,满足a1=1,Sn2-Sn-12=an3(n≥2).
(Ⅰ)求证数列{an}为等差数列,并求出其通项公式;
(Ⅱ)对于数列{an},在每两个ak与ak+1之间都插入k(k∈N+)个2,使数列{an}变成一个新数列{tm},数列{tm}的前m项和为Tm,若Tm>2014,求m的最小值.
(Ⅰ)求证数列{an}为等差数列,并求出其通项公式;
(Ⅱ)对于数列{an},在每两个ak与ak+1之间都插入k(k∈N+)个2,使数列{an}变成一个新数列{tm},数列{tm}的前m项和为Tm,若Tm>2014,求m的最小值.
考点:数列与不等式的综合,数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由已知,当n≥2时,(Sn+Sn-1)(Sn-Sn-1)=
,即(Sn+Sn-1)an=
,再写一式,两式相减,即可得出结论;
(Ⅱ)求出数列{tm}中,ak(含ak项)前的所有项之和,利用Tm>2014,求m的最小值.
| a | 3 n |
| a | 3 n |
(Ⅱ)求出数列{tm}中,ak(含ak项)前的所有项之和,利用Tm>2014,求m的最小值.
解答:
解:(Ⅰ)由已知,当n≥2时,(Sn+Sn-1)(Sn-Sn-1)=
,即(Sn+Sn-1)an=
,
∴Sn+Sn-1=
,Sn+1+Sn=
,两式相减得an+1+an=
-
,于是an+1-an=1(n≥2);
又由a1=1,
-
=
,可得a2=2,所以a2-a1=1;
因此,数列{an}是以1为首项,1为公差的等差数列,其通项公式为an=n.…6分
(Ⅱ)数列{tm}中,ak(含ak项)前的所有项之和为(1+2+…+k)+[1+2+…+(k-1)]×2=
+k(k-1)=
,
当k=36时,其和为
=1926<2014;当k=37时,其和为
=2035>2014;
又因为2014-1926=88>36×2=72,故恰好在k=37时开始满足Tm>2014.
∴mmin=37+(1+2+…+36)=703. …12分.
| a | 3 n |
| a | 3 n |
∴Sn+Sn-1=
| a | 2 n |
| a | 2 n+1 |
| a | 2 n+1 |
| a | 2 n |
又由a1=1,
| S | 2 2 |
| S | 2 1 |
| a | 3 2 |
因此,数列{an}是以1为首项,1为公差的等差数列,其通项公式为an=n.…6分
(Ⅱ)数列{tm}中,ak(含ak项)前的所有项之和为(1+2+…+k)+[1+2+…+(k-1)]×2=
| k(k+1) |
| 2 |
| 3k2-k |
| 2 |
当k=36时,其和为
| 3×362-36 |
| 2 |
| 3×372-37 |
| 2 |
又因为2014-1926=88>36×2=72,故恰好在k=37时开始满足Tm>2014.
∴mmin=37+(1+2+…+36)=703. …12分.
点评:本题考查等差数列的证明和通项公式的求法,考查实数取值范围的求法.考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
在空间四边形ABCD中,AB、BC、CD、DA上分别取E、F、G、H四点,如果EH、FG交于一点P,则( )
| A、P一定在直线BD上 |
| B、P一定在直线AC上 |
| C、P在直线AC或BD上 |
| D、P既不在直线BD上,也不在AC上 |
在数列{an}中,a1=2,an+1=an+ln(1+
),则an=( )
| 1 |
| n |
| A、2+ln n |
| B、2+(n-1)ln n |
| C、2+n ln n |
| D、1+n+ln n |
(x
-y
)6的展开式中x4y5的系数为( )
| y |
| x |
| A、20 | B、-20 |
| C、-15 | D、15 |
由y=ex、x轴、y轴及直线x=2围成的封闭图形的面积为( )
| A、e2 |
| B、e2-1 |
| C、e2+1 |
| D、e2ln2-1 |
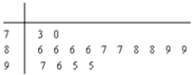 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):