题目内容
在空间四边形ABCD中,AB、BC、CD、DA上分别取E、F、G、H四点,如果EH、FG交于一点P,则( )
| A、P一定在直线BD上 |
| B、P一定在直线AC上 |
| C、P在直线AC或BD上 |
| D、P既不在直线BD上,也不在AC上 |
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:根据题意,可得直线EH、FG分别是平面ABD、平面BCD内的直线,因此EH、FG的交点必定在平面ABD和平面BCD的交线上.而平面ABD交平面BCD于BD,由此即可得到点P在直线BD上
解答:
解:∵点E、H分别在AB、AD上,而AB、AD是平面ABD内的直线,

∴E∈平面ABD,H∈平面ABD,可得直线EH?平面ABD,
∵点F、G分别在BC、CD上,而BC、CD是平面BCD内的直线,
∴F∈平面BCD,H∈平面BCD,可得直线FG?平面BCD,
因此,直线EH与FG的公共点在平面ABD与平面BCD的交线上,
∵平面ABD∩平面BCD=BD,
∴点P∈直线BD,
故选:A

∴E∈平面ABD,H∈平面ABD,可得直线EH?平面ABD,
∵点F、G分别在BC、CD上,而BC、CD是平面BCD内的直线,
∴F∈平面BCD,H∈平面BCD,可得直线FG?平面BCD,
因此,直线EH与FG的公共点在平面ABD与平面BCD的交线上,
∵平面ABD∩平面BCD=BD,
∴点P∈直线BD,
故选:A
点评:本题给出空间四边形,判断直线EH、FG的交点与已知直线BD的位置关系,着重考查了平面的基本性质和空间直线的位置关系判断等知识,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知P={x|y=
},Q={y|y=
},则下列结论正确的是( )
| x-1 |
| x-1 |
| A、P=Q | B、P∪Q=R |
| C、P?Q | D、Q?P |
数列1,x,x2,…xn-1前n项的和Sn=( )
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |
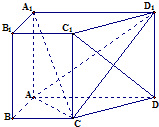 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD=
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD= 已知椭圆
已知椭圆