题目内容
5.已知a>0,函数y=x3-ax在区间[1,+∞)上是单调函数,则a的最大值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 法一:先利用导函数求出原函数的单调增区间,再让[1,+∞)是所求区间的子集可得结论.
法二:由题意a>0,函数f(x)=x3-ax,首先求出函数的导数,然后根据导数与函数单调性的关系进行判断.
解答 解:法一∵f(x)=x3-ax,
∴f′(x)=3x2-a=3(x-$\frac{\sqrt{a}}{3}$)(x+$\frac{\sqrt{a}}{3}$)
∴f(x)=x3-ax在(-∞,-$\frac{\sqrt{a}}{3}$),($\frac{\sqrt{a}}{3}$,+∞)上单调递增,
∵函数f(x)=x3-ax在[1,+∞)上单调,
∴$\frac{\sqrt{a}}{3}$≤1⇒a≤3
∴a的最大值为 3
法二:由法一得f′(x)=3x2-a,
∵函数f(x)=x3-ax在[1,+∞)上是单调函数,
根据二次函数的性质,显然是递增函数,
∴在[1,+∞)上,f′(x)≥0恒成立,
即a≤3x2在[1,+∞)上恒成立,
∴a≤3,
故选:D.
点评 本小题主要考查函数单调性的应用、函数导数与函数单调性之间的关系、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.极坐标方程ρ=2cosθ-4sinθ对应的直角坐标方程为( )
| A. | (x-1)2+(y+2)2=5 | B. | (x-1)2+(y-2)2=5 | C. | (x-2)2+(y-1)2=5 | D. | (x+1)2+(y+2)2=5 |
20.${({x^2}+\frac{1}{x}+1)^6}$的展开式中所有项的系数之和为( )
| A. | 81 | B. | 243 | C. | 729 | D. | 2187 |
10.复数$z=\frac{{{i^{2017}}}}{{1+{i^{2015}}}}$,则z在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.设A、B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧,在河岸边选定一点C,测出AC的距离是100m,∠BAC=60°,∠ACB=30°,则A、B两点的距离为( )
| A. | 40 m | B. | 50 m | C. | 60 m | D. | 70 m |
14.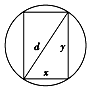 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )| A. | $\sqrt{3}$d,$\frac{\sqrt{3}}{3}$d | B. | $\frac{\sqrt{3}}{3}$d,$\frac{\sqrt{6}}{3}$d | C. | $\frac{\sqrt{6}}{3}$d,$\frac{\sqrt{3}}{3}$d | D. | $\frac{\sqrt{6}}{3}$d,$\sqrt{3}$d |
15.y=sin2x的图象向左平移$\frac{π}{4}$个单位,再向上平移1个单位,所得图象的函数解析式是( )
| A. | y=2cos2x | B. | y=2sin2x | C. | y=1+sin(2x+$\frac{π}{4}$) | D. | y=cos2x |